Bài tập 40 trang 27 SGK Toán 9 Tập 2

Lý thuyết5 Trắc nghiệm

18 BT SGK

563 FAQ

Giải bài 40 tr 27 sách GK Toán lớp 9 Tập 2

Giải các hệ phương trình sau và minh họa hình học kết quả tìm được:

a)\(\left\{ \matrix{2{\rm{x}} + 5y = 2 \hfill \cr {2 \over 5}x + y = 1 \hfill \cr} \right.\)

b) \(\left\{ \matrix{0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right.\)

c) \(\left\{ \matrix{{3 \over 2}x - y = {1 \over 2} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\)

Toán 9 Chương 3 Bài 7 Trắc nghiệm Toán 9 Chương 3 Bài 7 Giải bài tập Toán 9 Chương 3 Bài 7

Hướng dẫn giải chi tiết

Hướng dẫn giải

Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số để tìm nghiệm

Minh họa hình học: Tức là ta biểu thị 2 đường thẳng trên cùng hệ trục tọa độ.

Lời giải chi tiết

a) Giải hệ phương trình:

\(\left\{ \matrix{
2{\rm{x}} + 5y = 2(1) \hfill \cr
{2 \over 5}x + y = 1(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2{\rm{x}} + 5y = 2(1') \hfill \cr
- 2{\rm{x}} - 5y = - 5(2') \hfill \cr} \right.\)

Cộng (1’) với (2’) vế theo vế, ta được: \(0x + 0y = -3\)

Phương trình này vô nghiệm. Vậy hệ đã cho vô nghiệm.

Minh họa hình học kết quả tìm được:

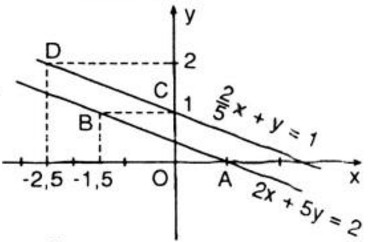
- Vẽ đồ thị hàm số \(2x + 5y = 2\).

Cho \(y = 0 ⇒ x = 1\). Ta xác định được điểm \(A(1; 0)\)

Cho \(y = 1 ⇒ x = -1,5\). Ta xác định được điểm \(B(-1,5; 1)\).

Đồ thị hàm số là đường thẳng đi qua hai điểm A và B

-Vẽ đồ thị hàm số \({2 \over 5}x + y = 1 \Leftrightarrow 2{\rm{x}} + 5y = 5\)

Cho \(x = 0 ⇒ y = 1\). Ta xác định được điểm \(C(0; 1)\)

Cho \(y = 2 ⇒ x = -2,5\). Ta xác định được điểm \(D(-2,5; 2)\)

Đồ thị hàm số là đường thẳng đi qua hai điểm C và D.

Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.

b) Giải hệ phương trình:

\(\left\{ \matrix{
0,2{\rm{x}} + 0,1y = 0,3(1) \hfill \cr
3{\rm{x}} + y = 5(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 2{\rm{x}} - y = - 3(1') \hfill \cr
3{\rm{x}} + y = 5(2') \hfill \cr} \right.\)

Cộng (1’) với (2’) vế theo vế, ta được \(x = 2\)

Thế \(x = 2\) vào (2), ta được: \(6 + y = 5 ⇔ y = -1\)

Vậy nghiệm của hệ phương trình là \((x = 2; y = -1)\)

Minh họa hình học:

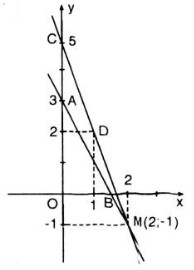
- Đồ thị hàm số \(0,2x + 0,1y = 0,3\) là một đường thẳng đi qua hai điểm:

\(A(x = 0; y = 3)\) và \(B(x = 1,5; y = 0)\)

- Đồ thị hàm số \(3x + y = 5\) là một đường thẳng đi qua hai điểm \(C(x = 0; y = 5)\) và \(D(x = 1; y = 2)\)

- Đồ thị hai hàm số trên cắt nhau tại điểm: \(M(x = 2; y = -1)\).

Vậy \((2; -1)\) là một nghiệm của hệ phương trình.

c) Giải hệ phương trình:

\(\left\{ \matrix{
{3 \over 2}x - y = {1 \over 2}(1) \hfill \cr
3{\rm{x}} - 2y = 1(2) \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 3{\rm{x}} + 2y = - 1(1') \hfill \cr
3{\rm{x}} - 2y = 1(2') \hfill \cr} \right.\)

Cộng (1’) và (2’) vế theo vế, ta có: \(0x + 0y = 0\).

Phương trình này có vô số nghiệm.

Nghiệm tổng quát là \(\left( {x;{3 \over 2}x - {1 \over 2}} \right)\) với \(x ∈ R\)

Minh họa hình học

- Đồ thị hàm số (1) là đường thẳng đi qua hai điểm \(A(0; - {1 \over 2})\) và \(B(1;1)\) nên hai đường thẳng này trùng nhau. Vậy hệ phương trinh có vô số nghiệm.

-- Mod Toán 9 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 40 trang 27 SGK Toán 9 Tập 2 HAY thì click chia sẻ

YOMEDIA