Bài tập 5 trang 114 SGK Hình học 11

Lý thuyết10 Trắc nghiệm

30 BT SGK

95 FAQ

Giải bài 5 tr 114 sách GK Toán Hình lớp 11

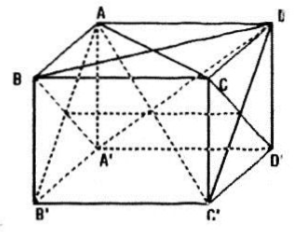
Cho hình lập phương ABCD.A'B'C'D'. Chứng minh rằng:

a) Mặt phẳng (AB'C'D) vuông góc với mặt phẳng (BCD'A');

b) Đường thẳng AC' vuông góc với mặt phẳng (A'BD).

Hình học 11 Bài 4 Trắc nghiệm Hình học 11 Bài 4 Giải bài tập Hình học 11 Bài 4

Hướng dẫn giải chi tiết

Câu a:

Vì ABB'A' là hình vuông \(\Rightarrow AB'\perp BA' \ (1)\)

Mặt khác \(\left.\begin{matrix} AD\perp AB\\ AD\perp AA' \end{matrix}\right\}\Rightarrow AD\perp (ABB'A')\)

\(\Rightarrow AD\perp BA' \ (2)\)

Từ (1) và (2) \(\Rightarrow BA'\perp (AB'C'D)\)

Mà \(BA'\subset (BCD'A')\) suy ra \((AB'C'D)\perp (BCD'A')\) (đpcm)

Câu b:

Ta có: \(\left.\begin{matrix} BD\perp AC\\ BD\perp CC' \end{matrix}\right\}\Rightarrow BD\perp (ACC'A')\)

\(\Rightarrow BD\perp AC' \ \ (1)\)

lại có \(A'B \perp AB'\) và \(B'C'\perp A'B\Rightarrow BA'\perp (AB'C'D) \Leftrightarrow BA'\perp AC' \ (2)\)

Từ (1) và (2) \(\Rightarrow AC' \perp (A'BD)\) (đpcm).

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 5 trang 114 SGK Hình học 11 HAY thì click chia sẻ

YOMEDIA

Cho các mệnh đề về đường thẳng, mệnh đề nào đúng?

bởi thu hằng 26/01/2021

A. Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

B. Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước.

C. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

D. Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

Theo dõi (0) 1 Trả lời
Khi nói về hai đường đường thẳng, thì mệnh đề nào sau đây là đúng?

bởi Chai Chai 25/01/2021

A. Hai đường thẳng không cắt nhau, không song song thì chéo nhau.

B. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song.

D. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.

Theo dõi (0) 1 Trả lời
Đâu là mệnh đề đúng trong các mệnh đề sau?

bởi Van Tho 26/01/2021

A. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia.

B. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau.

C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

D. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng sẽ vuông góc với mặt phẳng kia.

Theo dõi (0) 1 Trả lời
Chỉ ra mệnh đề đúng khi nói về đường thẳng và mặt phẳng trong các mệnh đề đã cho sau:

bởi can chu 25/01/2021

A. Cho hai đường thẳng song song a và b và đường thẳng c sao cho c ⊥ a, c ⊥ b. Mọi mặt phẳng (α) chứa c thì đều vuông góc với mặt phẳng (a; b)

B. Cho a ⊥ (α) , mọi mặt phẳng (β) chứa a thì (β) ⊥ (α) .

C. Cho a ⊥ b , mọi mặt phẳng chứa b đều vuông góc với a.

D. Cho a ⊥ b , nếu a ⊂ (α) và b ⊂ (β) thì (α) ⊥ (β) .

Theo dõi (0) 1 Trả lời