Bài tập 25 trang 112 SGK Hình học 11 NC

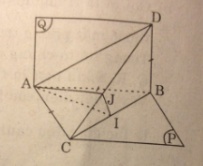
Gọi I là trung điểm của BC thì AI ⊥ BC.

Do BD ⊥ mp(ABC) nên AI ⊥ CD (định lí ba đường vuông góc).

Trong mp(CDB), kẻ IJ vuông góc với CD (J ϵ CD) thì mp(AIJ) chính là mặt phẳng (α) và thiết diện phải tìm là tam giác AIJ

Tam giác AIJ là tam giác vuông tại I.

Vậy \({S_{AIJ}} = \frac{1}{2}AI.IJ\)

Ta có:

\(\begin{array}{*{20}{l}}
{AI = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}}\\
\begin{array}{l}
\frac{{IJ}}{{DB}} = \frac{{CI}}{{CD}} \Rightarrow IJ = \frac{{CI}}{{CD}}.DB\\
 = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 3 }}.a = \frac{{a\sqrt 6 }}{6}
\end{array}
\end{array}\)

Vậy 

\({S_{AIJ}} = \frac{1}{2}.\frac{{a\sqrt 2 }}{2}.\frac{{a\sqrt 6 }}{6} = \frac{{{a^2}\sqrt 3 }}{{12}}\)

-- Mod Toán 11 HỌC247