Bài tập 10 trang 114 SGK Hình học 11

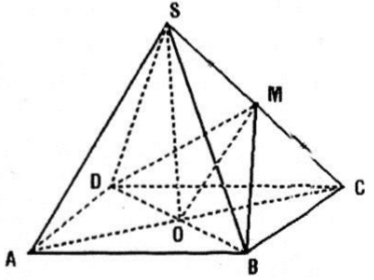
Câu a:

Ta có: \(AC=BD=a\sqrt{2}\Rightarrow AO=\frac{a\sqrt{2}}{2}\)

\(\Rightarrow SO=\sqrt{SA^2-AO^2}=\sqrt{a^2-\frac{2a^2}{4}}= \frac{a\sqrt{2}}{2}\)

Câu b:

Vì các cạnh bên và cạnh đáy đều bằng a nên các tam giác SBC và SDC là các tam giác đều; M là trung điểm SC ⇒ BM \(\perp\) SC và DM \(\perp\) SC.

\(\Rightarrow SC\perp (MBD);\) mà \(SC\subset (SAC)\)

\(\Rightarrow (MBD)\perp (SAC)\) (đpcm)

Câu c:

Vì BM là đường cao của tam giác đều cạnh a

\(\Rightarrow BM=\frac{a\sqrt{3}}{2}.\)

Trong tam giác vuông OMB ta có:

\(OM=\sqrt{MB^2-OB^2}=\sqrt{\frac{3a^2}{4}-\frac{2a^2}{4}}=\frac{a}{2}\)

Lại thấy: \(AC\perp BD\) và \(SO\perp AC\Rightarrow BD\perp (SAC)\); mà BD là giao tuyến của mặt phẳng (MBD) và mặt phẳng (ABCD) ⇒  góc MOC là góc giữa hai mặt phẳng (MBD) và (ABCD).

Trong tam giác vuông OSC có: \(OM=MS=MC=\frac{SC}{2}=\frac{a}{2}\)

\(\Rightarrow \Delta MOC\) là giác vuông cân \(\Rightarrow MOC =45^0\).

-- Mod Toán 11 HỌC247