Giải bài 3.24 tr 150 SBT Hình học 11
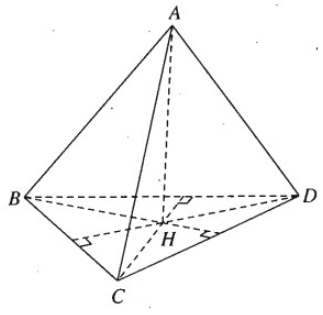
Chứng minh rằng nếu tứ diện ABCD có AB ⊥ CD và AC ⊥ BD thì AD ⊥ BC.
Hướng dẫn giải chi tiết
Vẽ AH ⊥ (BCD) tại H, ta có CD ⊥ AH và vì CD ⊥ AB ta suy ra CD ⊥ BH. Tương tự vì BD ⊥ AC ta suy ra BD ⊥ CH.
Vậy H là trực tâm của tam giác BCD tức là DH ⊥ BC.
Vì AH ⊥ BC nên ta suy ra BC ⊥ AD.
-- Mod Toán 11 HỌC247
-
Chứng minh BC vuông góc với mặt phẳng (OAH)?
bởi Như Quỳnh
05/06/2020
Giải giúp với
Theo dõi (1) 0 Trả lời -
Chứng minh rằng AB vuông góc với mf(BCD)?
bởi Như Quỳnh
05/06/2020
Giúp em giải bài này với ạ.
Theo dõi (1) 0 Trả lời -
Chứng minh H thuộc SI?
bởi Huỳnh Ngọc Bảo Hân
02/06/2020
Cho hình chóp S.ABC có SA vuông (ABC) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Chứng minh H thuộc SI ( với I là trung điểm BC)Theo dõi (0) 0 Trả lời -
Chứng minh (SIK) vuông góc (SCD)?
bởi LyHi
01/06/2020
Cho hình vuông ABCD cạnh a và tam giác SAB đều nằm trong 2 mặt phẳng vuông góc với nhau, gọi j là trung điểm AB, k là trung điểm CD.
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.22 trang 150 SBT Hình học 11
Bài tập 3.23 trang 150 SBT Hình học 11
Bài tập 2.25 trang 150 SBT Hình học 11
Bài tập 3.26 trang 151 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.28 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
