Giải bài 3.25 tr 150 SBT Hình học 11
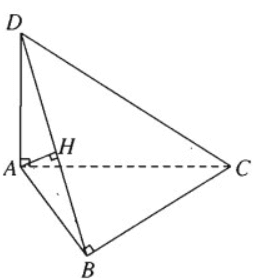
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD).
Từ điểm A trong mặt phẳng (ABD) ta vẽ AH vuông góc với BD, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Hướng dẫn giải chi tiết
Vì AD ⊥ (ABC) nên AD ⊥ BC.
Ngoài ra BC ⊥ AB nên ta có BC ⊥ (ABD).
Vì mặt phẳng (BCD) chứa BC mà BC ⊥ (ABD) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD. Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).
-- Mod Toán 11 HỌC247
-
Tính góc giữa hai mặt phẳng (SAD) và (SBC)?
bởi Vũ Hiệp
29/05/2020
Theo dõi (0) 0 Trả lời -
Chứng minh rằng (SAI) vuông góc (SBC)?
bởi Mai Đình Mẫn
29/05/2020
:33
Theo dõi (0) 0 Trả lời -
Cho hình chóp S.ABCD đáy ABCD là hình VUÔNG, SA⊥(ABCD). Chứng minh rằng: ( S A C ) ⊥ ( A B C D )
Theo dõi (0) 1 Trả lời -
Cho chóp SABCD đáy là hình vuông cạnh a. Hình chiếu vuông góc của S lên (ABCD) là trung điểm H của AB, tam giác ABC đều. Tính góc giữa (SAC) và (ABCD)
bởi Nguyễn Phương
15/05/2020
Theo dõi (0) 3 Trả lời
Bài tập SGK khác
Bài tập 3.23 trang 150 SBT Hình học 11
Bài tập 3.24 trang 150 SBT Hình học 11
Bài tập 3.26 trang 151 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.28 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
