Giải bài 3.26 tr 151 SBT Hình học 11
Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD);
b) Tam giác SBD là tam giác vuông tại S.
Hướng dẫn giải chi tiết
a) Gọi O là tâm của hình thoi, ta có AC ⊥ BD tại O
Vì SA = SC nên SO ⊥ AC.
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau (c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S.
-- Mod Toán 11 HỌC247
-
Tìm góc giữa hai mặt phẳng (SAC) và (ABCD)?
bởi Nguyễn Phương
15/05/2020
Theo dõi (0) 0 Trả lời -
Chứng minh (CDI) vuông góc (ABC) biết trong tứ diện ABCD có tam giác ABD cân tại D
bởi Diệu Em
09/05/2020
Chỉ mình bài này được không ạ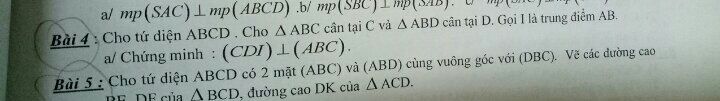
Theo dõi (0) 1 Trả lời -
Tính góc tạo bởi các mặt phẳng (ABC) và (BCD)?
bởi Khánh Vũ
26/04/2020
C60 or 61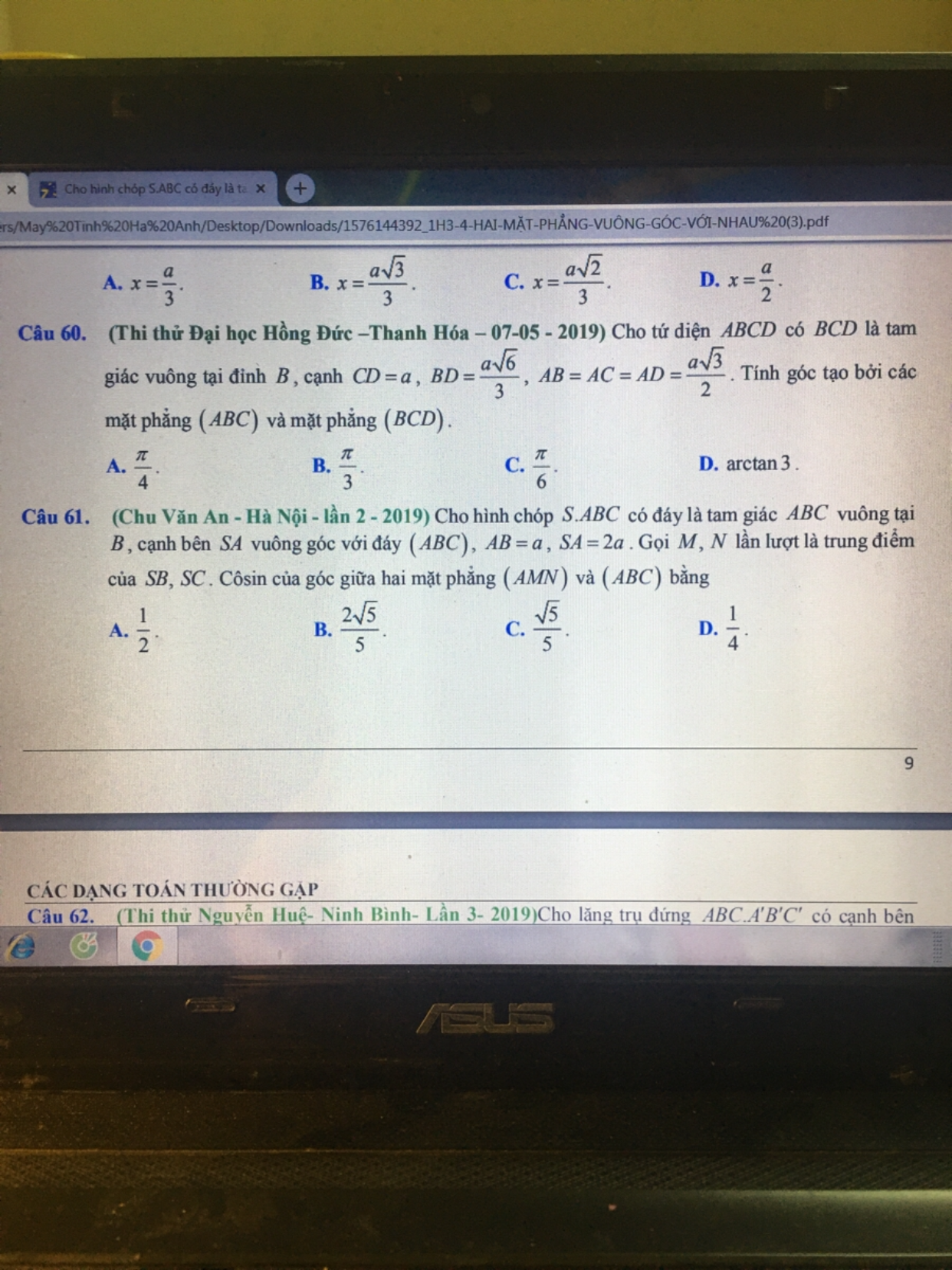
Theo dõi (0) 1 Trả lời -
Tìm góc giữa mặt phẳng SAB và mặt phẳng SAD
bởi Hoàng Khánh Ly
25/04/2020
Cho hình chóp SABCD có đáy là hình chữ nhật tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy Tìm góc giữa mặt phẳng SAB và mặt phẳng SADTheo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.24 trang 150 SBT Hình học 11
Bài tập 2.25 trang 150 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.28 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
