Bài tập 3.27 trang 151 SBT Hình học 11

30 BT SGK

Giải bài 3.27 tr 151 SBT Hình học 11

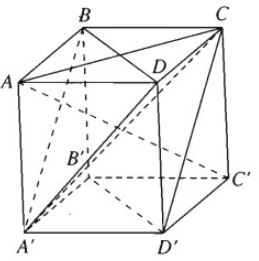
a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).

b) Tính đường chéo AC’ của hình lập phương đã cho.

Hình học 11 Bài 4 Trắc nghiệm Hình học 11 Bài 4 Giải bài tập Hình học 11 Bài 4

Hướng dẫn giải chi tiết

Giải sách bài tập Toán 11 | Giải sbt Toán 11

a) Ta có AB = AD = AA′ = a và C′B = C′D = C′A′ = $a\sqrt 2 $

Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’. Vậy AC′ ⊥ (BDA′). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà AC′ ⊥ (BDA′) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)

b) Ta có ACC’ là tam giác vuông có cạnh AC = $a\sqrt 2 $ và CC’ = a

Vậy AC′² = AC²+ CC′² ⇒ AC′² = 2a² + a²= 3a². Vậy AC′ = $a\sqrt 3 $.

-- Mod Toán 11 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 3.27 trang 151 SBT Hình học 11 HAY thì click chia sẻ

YOMEDIA

Xác định và tính thiết diện của hình chóp khi cắt bởi mp (a) qua AD vuông góc với (SBC)?

bởi Tử Linh 25/04/2020

Bài 3: cho hình chóp S.ABCD có đáy ABCD là hình thoi O, cạnh a, = 60^o; SO $⊥$ (ABCD), SO = $\frac{3 a/}{4}$ .

Xác định và tính thiết diện của hình chóp khi cắt bởi mp (a) qua AD vuông góc với (SBC).

Theo dõi (0) 0 Trả lời
Tính góc (SBC) và (SCD)?

bởi Khang Pham 24/04/2020

Giúp mình câu này với ạ

Theo dõi (0) 0 Trả lời
Chứng minh SO vuông góc vs mp(alpha) biết O là giao điểm của AC và BD, S là điểm nằm ngoài mp(alpha) sao cho SA = SC, SB = SD

bởi Mai Phương 20/04/2020

Trong mp(alpha) cho hình bình hành ABCD. Gọi O là giao điểm của AC và BD, S là điểm nằm ngoài mp(alpha) sao cho SA = SC, SB = SD. Chứng minh rằng: a) SOvuông góc vs mp(alpha) b) Nếu trong mp(SAB) kẻ SHvuông vs AB tại H thì AB vuông vs (SOH) c) Xác định và tính góc giữa cạnh bên SB và mp(ABCD), biết BD = 4 căn 3, SO = 2

Theo dõi (0) 1 Trả lời
Chứng minh rằng (AIA') vuông góc (BCC'B')?

bởi Jenny Phạm 19/04/2020

Giúp với ạ

Theo dõi (0) 2 Trả lời