Giải bài 4 tr 114 sách GK Toán Hình lớp 11
Cho hai mặt phẳng \((\alpha )\), \((\beta )\) cắt nhau và một điểm M không thuộc \((\alpha )\) và \((\beta )\). Chứng minh rằng qua điểm M có một và chỉ một mặt phẳng (P) vuông góc với \((\beta )\)và \((\beta )\). Nếu \((\alpha ) // (\beta )\) thì kết quả trên sẽ thay đổi như thế nào?
Hướng dẫn giải chi tiết
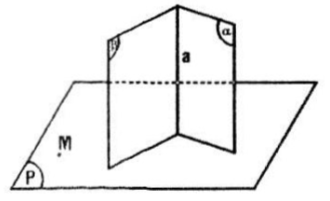
Ta có:
\(\left.\begin{matrix} (\alpha )\perp (P)\\ (\beta )\perp (P)\\ a=(\alpha )\cap (\beta ) \end{matrix}\right\}\Rightarrow a\perp (P)\)
Vì qua một điểm M cho trước có một và chỉ một mặt phẳng vuông góc với một đường thẳng cho trước nên qua M có một và chỉ một mặt phẳng (P) vuông góc với a.
Hay nói cách khác mặt phẳng (P) qua M vuông góc với \((\alpha )\) và \((\beta )\) là duy nhất.
* Nếu \((\alpha ) // (\beta )\) thì qua M có vô số mặt phẳng (P) vuông góc với cả \((\alpha )\) và \((\beta )\).
-- Mod Toán 11 HỌC247
-
Cho hình vuông ABCD. Dựng đoạn AS vuông góc với mặt phẳng chứa hình vuông ABCD. Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng SB, SC, SD và vuông góc với mặt phẳng (ABCD).
bởi Hương Lan
26/02/2021
Theo dõi (0) 1 Trả lời -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a SA vuông góc vs mp ( ABCD ) , SA = a √6 . a. Chứng minh rằng CD vuông góc vs mp ( SAD ).
bởi Nguyễn Thanh Tâm
09/02/2021
Câu 3. Cho hình chóp S.ABCD có đáy là hình vuông cạnh a SA vuông góc vs mp ( ABCD ) , SA = a √6 .
a , Chứng minh rằng CD vuông góc vs mp ( SAD ) .
b , Chứng minh rằng SC vuông góc vs BD .
c . Tính góc giữa đường thẳng SC và đáy .
Theo dõi (0) 0 Trả lời -
Cho chóp SABC có đáy là tam giác vuông cân tại B, SA vuông góc với đáy và SA=SB=SC=a. H là trung điểm AC, BK là đường cao của tam giác SBC
bởi Đào Mạnh
07/02/2021
a) Chứng minh BH vuông góc (SAC),SC vuông góc (BHK)b) Tính các cạnh và diện tích của tam giác BHK
Theo dõi (0) 0 Trả lời -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm SB và SD. Sin của góc giữa hai mặt phẳng (AMN) và (SBD) bằng?
bởi Nhi Nhi
06/02/2021
Cho hình chóp S.ABCD có đáy là hình vuông cạnh $#a, cạnh bên SA=a và vuông góc với mặt phẳng đáy. Gọi M,N lần lượt là trung điểm SB và SD. Sin của góc giữa hai mặt phẳng (AMN) và (SBD) bằng?
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 2 trang 113 SGK Hình học 11
Bài tập 3 trang 113 SGK Hình học 11
Bài tập 5 trang 114 SGK Hình học 11
Bài tập 6 trang 114 SGK Hình học 11
Bài tập 7 trang 114 SGK Hình học 11
Bài tập 8 trang 114 SGK Hình học 11
Bài tập 9 trang 114 SGK Hình học 11
Bài tập 10 trang 114 SGK Hình học 11
Bài tập 11 trang 114 SGK Hình học 11
Bài tập 3.22 trang 150 SBT Hình học 11
Bài tập 3.23 trang 150 SBT Hình học 11
Bài tập 3.24 trang 150 SBT Hình học 11
Bài tập 2.25 trang 150 SBT Hình học 11
Bài tập 3.26 trang 151 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.28 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
