Bài tập 27 trang 112 SGK Hình học 11 NC

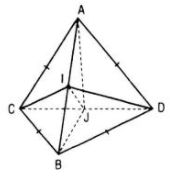
a) Vì J là trung điểm của CD và AC = AD nên AJ ⊥ CD.

Do mp(ACD) ⊥ mp(BCD) nên AJ ⊥ mp(BCD)

Mặt khác, AC = AD = BC = BD nên tam giác AJB vuông cân

Suy ra \(AB = AJ\sqrt 2 ,A{J^2} = {a^2} - {x^2}\)

Hay \(AJ = \sqrt {{a^2} - {x^2}} .\)

Vậy \(AB = \sqrt {2\left( {{a^2} - {x^2}} \right)} \) với a > x

Do IA = IB, tam giác AJB vuông tại J

Nên \(JI = \frac{1}{2}AB,\), 

Tức là \(IJ = \frac{1}{2}\sqrt {2({a^2} - {x^2})} \)

b) CI và DI vuông góc với AB.

Vậy mp(ABC) ⊥ mp(ABD) \( \Leftrightarrow \widehat {CID} = {90^0}\)

\(\begin{array}{*{20}{l}}
\begin{array}{l}
 \Leftrightarrow IJ = \frac{1}{2}CD\\
 \Leftrightarrow \frac{1}{2}\sqrt {2({a^2} - {x^2})}  = \frac{1}{2}.2x
\end{array}\\
{ \Leftrightarrow x = \frac{{a\sqrt 3 }}{3}}
\end{array}\)

-- Mod Toán 11 HỌC247