Giải bài 3.23 tr 150 SBT Hình học 11
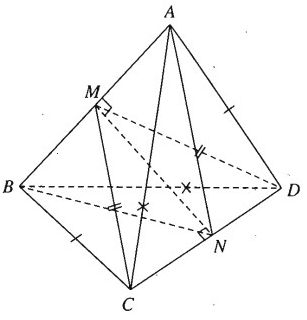
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Hướng dẫn giải chi tiết
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
-- Mod Toán 11 HỌC247
-
Tính góc giữa hai mặt phẳng (SAC) và (SBC)?
bởi Trần Thị Thùy Dương
16/06/2020
Theo dõi (0) 2 Trả lời -
Tính góc giữa mặt bên (SBC) và mặt đáy (ABCD)?
bởi Liên Ngọc
14/06/2020
Giúp mình 2 câu này với
Theo dõi (0) 0 Trả lời -
Tính góc giữa hai mặt phẳng (SIC) và (ABC)?
bởi Nguyễn Vinh
14/06/2020
Câu 5
Theo dõi (0) 0 Trả lời -
Tính góc giữa đường thẳng SB với mặt phẳng (SAC)?
bởi Như Quỳnh
05/06/2020
Giúp em giải bài này đi ạ.
Theo dõi (1) 0 Trả lời
Bài tập SGK khác
Bài tập 11 trang 114 SGK Hình học 11
Bài tập 3.22 trang 150 SBT Hình học 11
Bài tập 3.24 trang 150 SBT Hình học 11
Bài tập 2.25 trang 150 SBT Hình học 11
Bài tập 3.26 trang 151 SBT Hình học 11
Bài tập 3.27 trang 151 SBT Hình học 11
Bài tập 3.28 trang 151 SBT Hình học 11
Bài tập 3.29 trang 151 SBT Hình học 11
Bài tập 3.30 trang 151 SBT Hình học 11
Bài tập 3.31 trang 151 SBT Hình học 11
Bài tập 3.32 trang 152 SBT Hình học 11
Bài tập 21 trang 111 SGK Hình học 11 NC
Bài tập 22 trang 111 SGK Hình học 11 NC
Bài tập 23 trang 111 SGK Hình học 11 NC
Bài tập 24 trang 111 SGK Hình học 11 NC
Bài tập 25 trang 112 SGK Hình học 11 NC
Bài tập 26 trang 112 SGK Hình học 11 NC
