Bài tập 22 trang 111 SGK Hình học 11 NC
Cho hình hộp ABCD.A’B’C’D’ có AB = a, BC = b, CC’ = c. Nếu \(AC\prime = BD\prime = B\prime D = \sqrt {{a^2} + {b^2} + {c^2}} \)
Thì hình hộp đó có phải là hình hộp chữ nhật không ? Vì sao ?
Hướng dẫn giải chi tiết
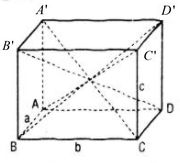
Áp dụng tính chất : “Tổng bình phương hai đường chéo hình bình hành bằng tổng bình phương bốn cạnh của nó”
Ta có:
\(\begin{array}{*{20}{l}}
{AC{\prime ^2} + A\prime {C^2} = 2(AA{\prime ^2} + A\prime {C^2})}\\
{B\prime {D^2} + BD{\prime ^2} = 2(BB{\prime ^2} + B{D^2})}\\
{ \Rightarrow AC{\prime ^2} + A\prime {C^2} + BD{\prime ^2} + B\prime {D^2}}\\
\begin{array}{l}
= 2({c^2} + {c^2} + A{C^2} + B{D^2})\\
= 4({a^2} + {b^2} + {c^2})
\end{array}\\
{ \Rightarrow A\prime C = AC\prime = B\prime D = BD\prime }
\end{array}\)
⇒ AA’C’C và BB’D’D là các hình chữ nhật
Từ đó suy ra AA’ ⊥ AC và AA’ ⊥ BD.
Do đó AA’ ⊥ (ABCD), tức hình hộp ABCD.A’B’C’D’ là hình hộp chữ nhật.
-- Mod Toán 11 HỌC247
-


Chứng minh mp AHK vuông góc với mp SAC
bởi Lan Anh
 24/10/2018
24/10/2018
Cho hình chóp S.ABCD đáy là hinh chữ nhật có SA vuông gốc với đáy.
a) CM: (SBC) VUÔNG GỐC (SAB)
(SCD) VUONG GỐC (SAD)
b) H và K là hình chiếu vuông gốc của A lên SB và SD. CM: (AHK) VUÔNG GỐC (SAC)
Theo dõi (0) 1 Trả lời -


Tính góc giữa (SBD) và (ABCD) biết đường thẳng SO vông góc với đáy và SO=a căn 3/2
bởi Nguyễn Thị Lan
 03/04/2018
03/04/2018
cho hình chóp SABCD có đấy ABCD hình vuông tâm O cạnh a.đường thẳng SO vông góc với đáy và SO=a*căn 3/2 tính góc giữa (SBD) và (ABCD)
Theo dõi (0) 1 Trả lời -


Chứng minh hai mặt phẳng (SAB) và (SAC) vuông góc biết tam giác đều ABC, cạnh a
bởi Lê Khánh Huyền
 14/11/2017
14/11/2017
Cho tam giác đều ABC, cạnh a. Gọi D là điểm đối xứng với A qua BC. Trên đường thẳng vuông góc vơi mp(ABC) tại D lấy điểm S sao cho SD = a6–√. Chứng minh hai mặt phẳng (SAB) và (SAC) vuông góc với nhau.
Theo dõi (0) 1 Trả lời





