Bài tập 24 trang 111 SGK Hình học 11 NC
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và SA ⊥ (ABCD), SA = x. Xác định x để hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 600
Hướng dẫn giải chi tiết
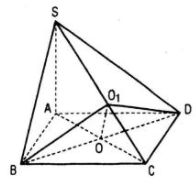
Gọi O là giao điểm của AC và BD.
Trong mặt phẳng (SAC) kẻ OO1 vuông góc với SC, dễ thấy mp(BO1D) vuông góc với SC.
Vậy góc giữa hai mp(SBC) và (SDC) bằng góc giữa hai đường thẳng BO1 và DO1.
Mặt khác OO1 ⊥ BD, OO1 < OC mà OC = OB nên \(\widehat {B{O_1}O} > {45^0}\)
Tương tự \(\widehat {D{O_1}O} > {45^0}\) tức \(\widehat {B{O_1}D} > {90^0}\)
Như vậy hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 600 khi và chỉ khi:
\(\widehat {B{O_1}D} = {120^0} \Leftrightarrow \widehat {B{O_1}O} = {60^0}\)
(vì ΔBO1D cân tại O1)
\( \Leftrightarrow BO = O{O_1}tan{60^0} \Leftrightarrow BO = O{O_1}\sqrt 3 \)
Ta lại có
\(\begin{array}{l}
O{O_1} = OC\sin \widehat {OC{O_1}}\\
= OC\sin \widehat {ACS} = OC.\frac{{SA}}{{SC}}
\end{array}\)
Như vậy: \(BO = O{O_1}\sqrt 3 \)
\(\Leftrightarrow BO = \sqrt 3 .OC.\frac{{SA}}{{SC}} \)
\(\Leftrightarrow SC = \sqrt 3 .SA\)
\( \Leftrightarrow \sqrt {{x^2} + 2{a^2}} = \sqrt 3 .x \Leftrightarrow x = a\)
Vậy khi x = a thì hai mặt phẳng (SBC) và (SDC) tạo với nhau góc 600.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





