Giải bài 3.5 tr 164 SBT Toán 12
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
a) \(\smallint (1 - 2x)exdx\)
b) \(\smallint xe - xdx\)
c) \(\smallint x\ln (1 - x)dx\)
d) \(\smallint x\sin 2xdx\)
Hướng dẫn giải chi tiết
a) \(I = \mathop \smallint \nolimits \left( {1 - 2x} \right){e^x}dx\)
Đặt \(\left\{ \begin{array}{l}
u = 1 - 2x\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = - 2dx\\
v = {e^x}
\end{array} \right.\)
Ta có:
\({I = \left( {1 - 2x} \right){e^x} + \mathop \smallint \nolimits 2{e^x}dx + C = {e^x} - 2x{e^x} + 2{e^x} + C = \left( {3 - 2x} \right){e^x} + C}\)
b) \(J = \mathop \smallint \nolimits x{e^{ - x}}dx\)
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = {e^{ - x}}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = - {e^{ - x}}
\end{array} \right.\)
Ta có:
\({I = - x{e^{ - x}} + \mathop \smallint \nolimits {e^{ - x}}dx + C = - x{e^{ - x}} - {e^{ - x}} + C = - \left( {1 + x} \right){e^{ - x}} + C}\)
c) \(G = \mathop \smallint \nolimits x\ln \left( {1 - x} \right)dx\)
Đặt \(\left\{ \begin{array}{l}
u = \ln \left( {1 - x} \right)\\
dv = xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = \frac{1}{{x - 1}}dx\\
v = \frac{{{x^2}}}{2}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
G = \frac{{{x^2}}}{2}\ln \left( {1 - x} \right) - \frac{1}{2}\int {\frac{{{x^2}}}{{x - 1}}} dx\\
= \frac{{{x^2}}}{2}\ln \left( {1 - x} \right) - \frac{1}{2}\int {\left( {x + 1 + \frac{1}{{x - 1}}} \right)} dx\\
= \frac{{{x^2}}}{2}\ln \left( {1 - x} \right) - \frac{1}{2}\left[ {\frac{{{x^2}}}{2} + x + \ln \left( {1 - x} \right)} \right] + C\\
= \frac{{{x^2}}}{2}\ln \left( {1 - x} \right) - \frac{1}{2}\ln \left( {1 - x} \right) - \frac{1}{4}{x^2} - \frac{1}{2}x + C
\end{array}\)
d) Ta có:
\(H = \mathop \smallint \nolimits x{\sin ^2}xdx = \mathop \smallint \nolimits x.\frac{{1 - cos2x}}{2}dx = \frac{{{x^2}}}{4} - \frac{1}{2}\mathop \smallint \nolimits^ x\cos 2xdx = \frac{{{x^2}}}{4} - \frac{1}{2}I\)
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = \cos 2xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = \frac{1}{2}\sin 2x
\end{array} \right.\)
Suy ra:
\({I = \frac{1}{2}x\sin 2x - \frac{1}{2}\mathop \smallint \nolimits \sin 2xdx = \frac{1}{2}x\sin 2x + \frac{1}{4}\cos 2x + C}\)
Vậy \(H = \frac{{{x^2}}}{4} - \frac{1}{2}\left( {\frac{1}{2}x\sin 2x + \frac{1}{4}\cos 2x} \right) + C\)
-- Mod Toán 12 HỌC247
-


Hãy tính: \(∫{(1-x)}^9dx\), (đặt \(u =1-x\) ).
bởi thu trang
 05/05/2021
05/05/2021
Hãy tính: \(∫{(1-x)}^9dx\), (đặt \(u =1-x\) ).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) =\dfrac{1}{(1+x)(1-2x)}\) .
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) = e^{3-2x}\).
bởi Bo Bo
 05/05/2021
05/05/2021
Hãy tìm nguyên hàm của hàm số sau: \(f(x) = e^{3-2x}\).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) = tan^2x\).
bởi can chu
 06/05/2021
06/05/2021
Hãy tìm nguyên hàm của hàm số sau: \(f(x) = tan^2x\).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) = sin5x.cos3x\).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) = \dfrac{1}{sin^{2}x.cos^{2}x}\).
bởi Nguyễn Thị Lưu
 05/05/2021
05/05/2021
Hãy tìm nguyên hàm của hàm số sau: \(f(x) = \dfrac{1}{sin^{2}x.cos^{2}x}\).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \( f(x)=\dfrac{2^{x}-1}{e^{x}}\).
Theo dõi (0) 1 Trả lời -


Hãy tìm nguyên hàm của hàm số sau: \(f(x) = \dfrac{x+\sqrt{x}+1}{^{\sqrt[3]{x}}}\).
bởi Mai Hoa
 05/05/2021
05/05/2021
Hãy tìm nguyên hàm của hàm số sau: \(f(x) = \dfrac{x+\sqrt{x}+1}{^{\sqrt[3]{x}}}\).
Theo dõi (0) 1 Trả lời -


Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \((1-\dfrac{2}{x})^{2}e^{x}\) và \((1-\dfrac{4}{x})e^{x}\).
bởi Dương Quá
 06/05/2021
06/05/2021
Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \((1-\dfrac{2}{x})^{2}e^{x}\) và \((1-\dfrac{4}{x})e^{x}\).
Theo dõi (0) 1 Trả lời -


Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \(\sin 2x\) và \(\sin^2x\) .
bởi minh dương
 05/05/2021
05/05/2021
Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \(\sin 2x\) và \(\sin^2x\) .
Theo dõi (0) 1 Trả lời -


Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \(e^{-x}\) và \(- e^{-x}\).
bởi Phan Thiện Hải
 05/05/2021
05/05/2021
Nhận xét hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số còn lại: \(e^{-x}\) và \(- e^{-x}\).
Theo dõi (0) 1 Trả lời -


Hãy tính \(\smallint x\sin xdx.\)
bởi het roi
 06/05/2021
06/05/2021
Hãy tính \(\smallint x\sin xdx.\)
Theo dõi (0) 1 Trả lời -


Hãy tính: \(\smallint \cos xdx\)
bởi Minh Tú
 06/05/2021
06/05/2021
Hãy tính: \(\smallint \cos xdx\)
Theo dõi (0) 1 Trả lời -


Hãy tính: \(\smallint \left( {x\cos x} \right)'dx\)
bởi Mai Rừng
 05/05/2021
05/05/2021
Hãy tính: \(\smallint \left( {x\cos x} \right)'dx\)
Theo dõi (0) 1 Trả lời -


Cho \(\displaystyle \int {{{\ln x} \over x}} dx\). Đặt \(x=e^t\), hãy viết \(\displaystyle\int {{{\ln x} \over x}} dx\) theo \(t\) và \(dt\)
bởi Dương Minh Tuấn
 06/05/2021
06/05/2021
\(\displaystyle \int {{{\ln x} \over x}} dx\). Đặt \(x=e^t\), hãy viết \(\displaystyle\int {{{\ln x} \over x}} dx\) theo \(t\) và \(dt\)
Theo dõi (0) 1 Trả lời -


Có \(\smallint {\left( {x{\rm{ }} - {\rm{ }}1} \right)^{10}}dx\). Đặt \(u = x – 1\), hãy viết \({\left( {x{\rm{ }} - {\rm{ }}1} \right)^{10}}dx\) theo \(u\) và \(du\).
bởi Phí Phương
 06/05/2021
06/05/2021
Cho \(\smallint {\left( {x{\rm{ }} - {\rm{ }}1} \right)^{10}}dx\). Đặt \(u = x – 1\), hãy viết \({\left( {x{\rm{ }} - {\rm{ }}1} \right)^{10}}dx\) theo \(u\) và \(du\).
Theo dõi (0) 1 Trả lời -


Tính nguyên hàm của hàm số
bởi Truong Nhi
 22/04/2021
22/04/2021
Giúp em với ạ
Theo dõi (1) 1 Trả lời -


Tìm nguyên hàm e^lnx/x dx
bởi Thảo Vy
 21/04/2021
Tìm nguyên hàmTheo dõi (0) 1 Trả lời
21/04/2021
Tìm nguyên hàmTheo dõi (0) 1 Trả lời -


Tính nguyên hàm của e^2x.sin3x
bởi Diệp Châu Hòann
 21/03/2021
21/03/2021
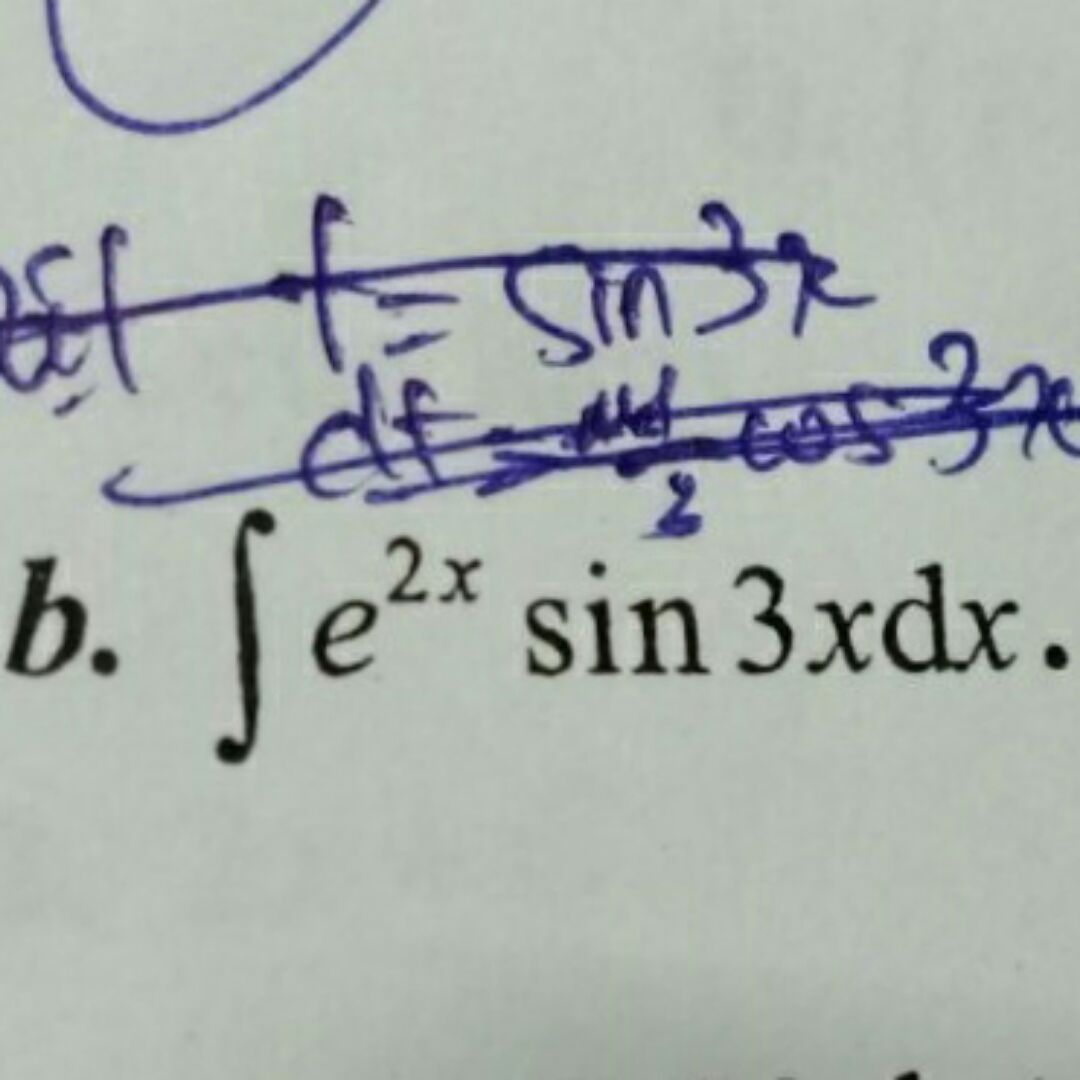 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Một nguyên hàm của 2cosxf xxlà
bởi Nguyễn Phúc Trường
 22/02/2021
Một nguyên hàm của 2cosxf xxlàTheo dõi (0) 1 Trả lời
22/02/2021
Một nguyên hàm của 2cosxf xxlàTheo dõi (0) 1 Trả lời -


Nguyên hàm của 1 trừ cos 2x chia 2
bởi Trần Thị Thùy Trâm
 22/02/2021
Nguyên hàm của 1 - cos2x 2Theo dõi (0) 2 Trả lời
22/02/2021
Nguyên hàm của 1 - cos2x 2Theo dõi (0) 2 Trả lời -


Hàm số F(x) nào sau đây là một nguyên hàm của hàm của hàm số f(x).g(x) biết F(1)=3
bởi Nguyên Hồ
 19/02/2021
19/02/2021
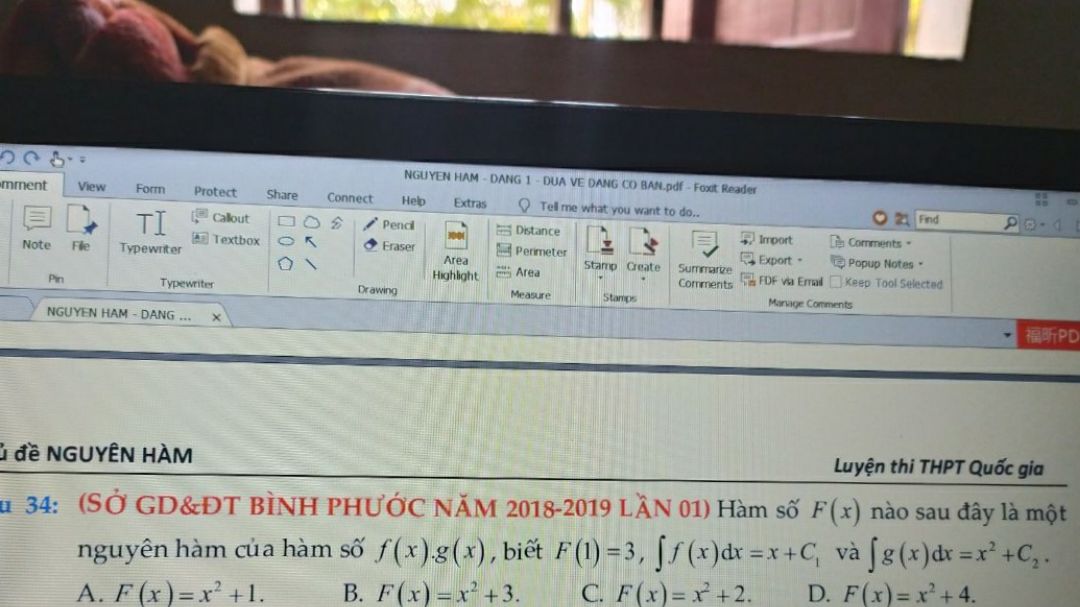 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của x^3×e^x nhân dx
bởi Trần Đại
 25/01/2021
Mọi người giải giúp em với ạ
25/01/2021
Mọi người giải giúp em với ạ Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm của hàm số sau.
bởi Triệu Duy Bảo
 18/01/2021
Tìm nguyên hàm của hàm số sau
18/01/2021
Tìm nguyên hàm của hàm số sau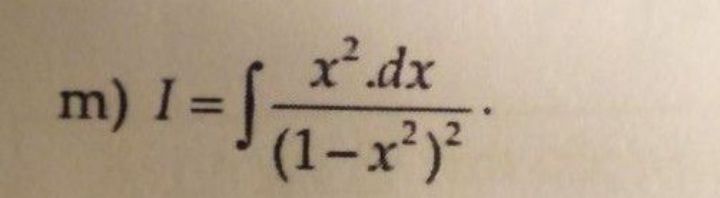 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.3 trang 164 SBT Toán 12
Bài tập 3.4 trang 164 SBT Toán 12
Bài tập 3.6 trang 164 SBT Toán 12
Bài tập 3.7 trang 164 SBT Toán 12
Bài tập 3.8 trang 165 SBT Toán 12
Bài tập 3.9 trang 165 SBT Toán 12
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.11 trang 165 SBT Toán 12
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC






