Giải bài 3.8 tr 165 SBT Toán 12
Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của hàm số
\(f(x) = \frac{1}{{1 + \sin x}}?\)
a) \(F\left( x \right) = 1 - \cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right)\)
b) \(G(x) = 2\tan \frac{x}{2}\)
c) \(H(x) = \ln (1 + \sin x)\)
d) \(K(x) = 2\left( {1 - \frac{1}{{1 + \tan \frac{x}{2}}}} \right)\)
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{l}
\int {\frac{1}{{1 + \sin x}}dx} = \int {\frac{1}{{{{\left( {\sin \frac{x}{2} + \cos \frac{x}{2}} \right)}^2}}}dx} \\
= \int {\frac{1}{{2{{\sin }^2}\left( {\frac{x}{2} + \frac{\pi }{4}} \right)}}dx} = - \cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right) + C
\end{array}\)
Vậy \(F\left( x \right) = 1 - \cot \left( {\frac{x}{2} + \frac{\pi }{4}} \right)\) là một nguyên hàm của hàm số f(x).
\(G'(x) = \frac{1}{{\tan \frac{x}{2}}} = \frac{{\cos \frac{x}{2}}}{{\sin \frac{x}{2}}} = \frac{{2{{\cos }^2}\frac{x}{2}}}{{\sin x}}\) nên G(x) không là nguyên hàm của hàm số f(x)
\(H'(x) = \frac{{(1 + \sin x)'}}{{1 + \sin x}} = \frac{{\cos x}}{{1 + \sin x}}\) nên H(x) không là nguyên hàm của hàm số f(x).
\(\begin{array}{l}
K'\left( x \right) = 2.\frac{{{{\left( {1 + \tan \frac{x}{2}} \right)}^\prime }}}{{{{\left( {1 + \tan \frac{x}{2}} \right)}^2}}} = 2.\frac{{\frac{1}{{2{{\cos }^2}\frac{x}{2}}}}}{{{{\left( {\frac{{\cos \frac{x}{2} + \sin \frac{x}{2}}}{{\cos \frac{x}{2}}}} \right)}^2}}}\\
= \frac{1}{{{{\left( {\cos \frac{x}{2} + \sin \frac{x}{2}} \right)}^2}}} = \frac{1}{{1 + \sin x}}
\end{array}\)
Vậy K(x) là một nguyên hàm của hàm số f(x).
-- Mod Toán 12 HỌC247
-


Tìm nguyên hàn của hàm số f(x)=e^x^2
bởi Yến Nguyễn
 11/04/2020
f(x)=e^x^2 tìm nguyên hàn của hàm sốTheo dõi (0) 1 Trả lời
11/04/2020
f(x)=e^x^2 tìm nguyên hàn của hàm sốTheo dõi (0) 1 Trả lời -


Tìm nguyên hàm của (1+sinx)^2
bởi Thư Võ
 11/04/2020
11/04/2020
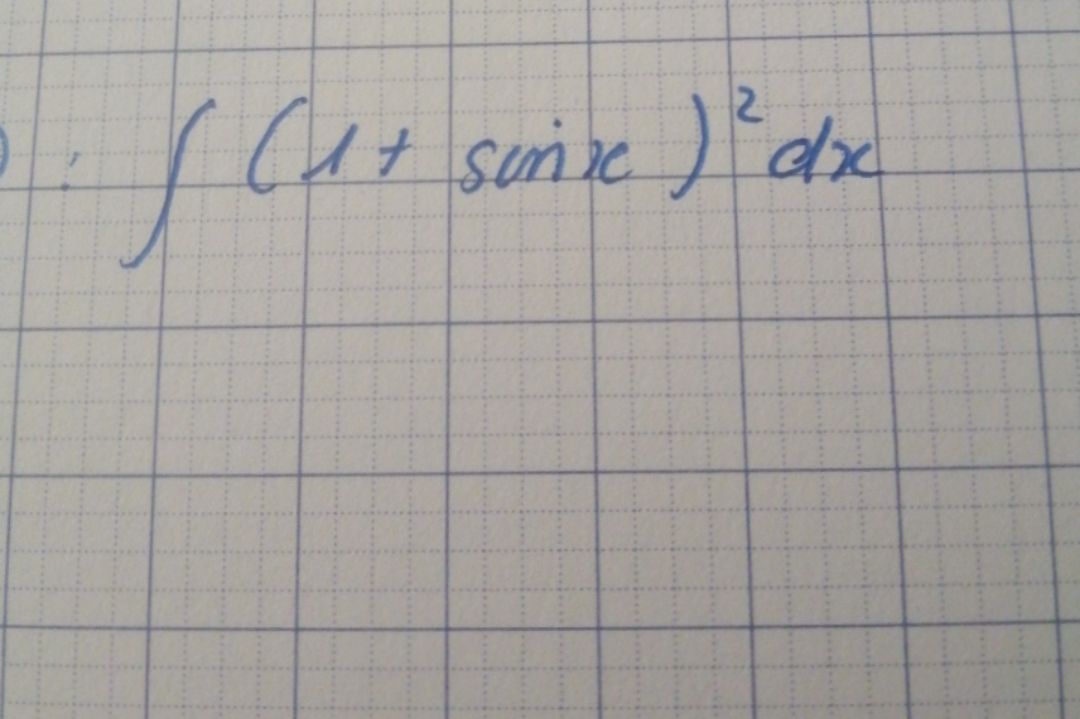 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tìm nguyên hàm của sin5x.sinx
bởi trần phương
 09/04/2020
Tìm nguyên hàm của sin5x.sinxTheo dõi (0) 3 Trả lời
09/04/2020
Tìm nguyên hàm của sin5x.sinxTheo dõi (0) 3 Trả lời -


Nguyên hàm I= 1/(4 - x)^2dx
bởi Đỗ Thuỳ Liên
 09/04/2020
09/04/2020
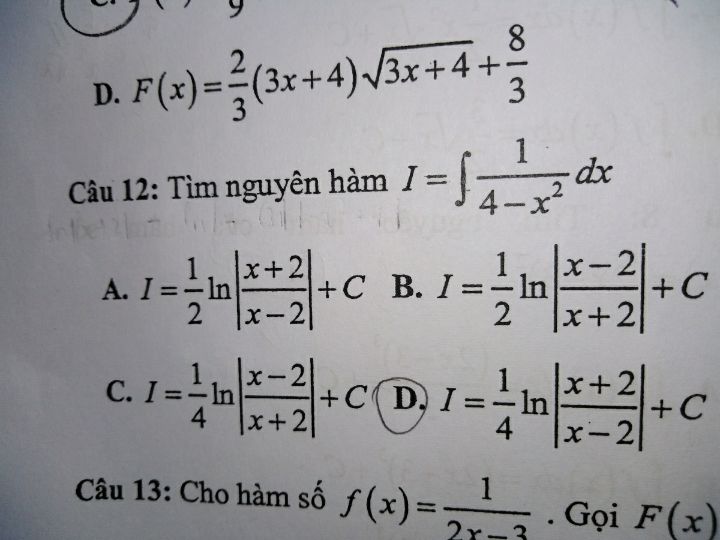 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Họ nguyên hàm của hàm số f(x)=(2x-1)lnx
bởi Hồ Đức Duy
 08/04/2020
08/04/2020
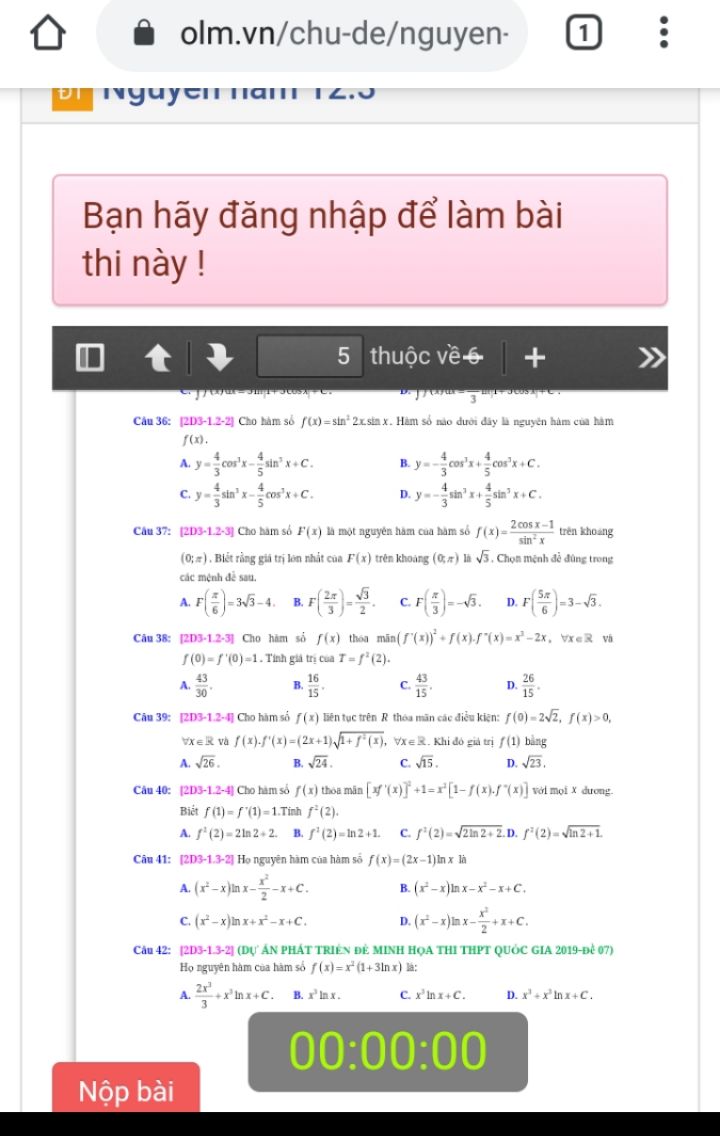 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Họ các nguyên hàm của hàm số f(x)=x^3-9
bởi Lan Phùng
 05/04/2020
05/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tính nguyên hàm xsin2xdx
bởi liuhinngoc
 04/04/2020
04/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Nguyên hàm của hàm số f(x)=x^3-3/x^2 2x
bởi liuhinngoc
 04/04/2020
Nguyên ham cua ham so f(x)=x^3-3/x^2 2x làTheo dõi (0) 2 Trả lời
04/04/2020
Nguyên ham cua ham so f(x)=x^3-3/x^2 2x làTheo dõi (0) 2 Trả lời -


Tính nguyên hàm của 1/x+x
bởi Thơm Mắm
 02/04/2020
02/04/2020
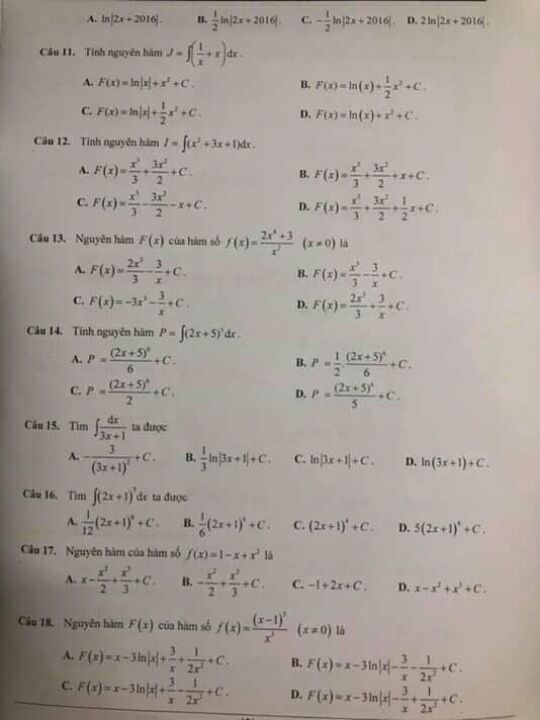 Theo dõi (0) 17 Trả lời
Theo dõi (0) 17 Trả lời -


Tính nguyên hàm của x căn bậc bốn của 1-x^2
bởi Ánh Ngọc Vũ
 27/03/2020
27/03/2020
.jpg) hbiuuiuuuuuTheo dõi (0) 2 Trả lời
hbiuuiuuuuuTheo dõi (0) 2 Trả lời -


Tìm đạo hàm của hàm số y= 3^-x
bởi Ngọc Diễm
 27/03/2020
Toán
27/03/2020
Toán Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Hàm số f(x)=(9x-10)/(6x^2-11x+3) có một nguyên hàm là F(x) thỏa mãn F(1)=ln2. Gọi x1, x2 là hai nghiệm của phương trình F(x)=ln|3x-1|+1/2ln3. Tính 3^x1+3^x2
bởi Huy Thanh
 26/03/2020
o
26/03/2020
o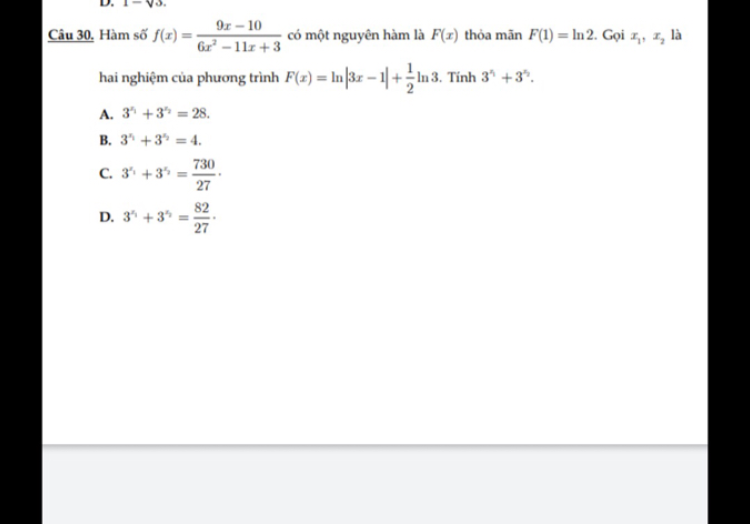 Theo dõi (0) 12 Trả lời
Theo dõi (0) 12 Trả lời -


Tính nguyên hàm của hàm số 1/(3-2x)^5
bởi Mai Khánh My Ngô
 26/03/2020
Mọi người giải giúp em câu 1 d với ạ
26/03/2020
Mọi người giải giúp em câu 1 d với ạ Theo dõi (0) 11 Trả lời
Theo dõi (0) 11 Trả lời -


Cho hàm số f(x)=2x+1/căn(2x-3). F(x)=(ax+b).(2x-3)^(-3/2) với x>3/2. Tìm a, b để hàm số F(x) là một nguyên hàm của hàm số f(x).
bởi Vũ Ngọc Huyền
 24/03/2020
24/03/2020
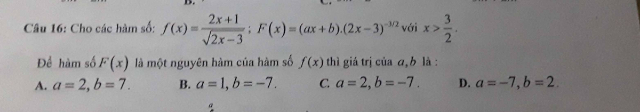 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của f(x)=2x+1/x+e^(3x)
bởi Thu Lê
 24/03/2020
Làm giúp e với
24/03/2020
Làm giúp e với Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Họ nguyên hàm của hàm số xe^x
bởi Minh Nguyễn
 19/03/2020
19/03/2020
Họ nguyên hàm của hàm số xe^x
Theo dõi (0) 5 Trả lời -


Tìm nguyên hàm của (2xln(x^2+1))/(x^2+1)
bởi Thiêên Kim
 18/03/2020
18/03/2020
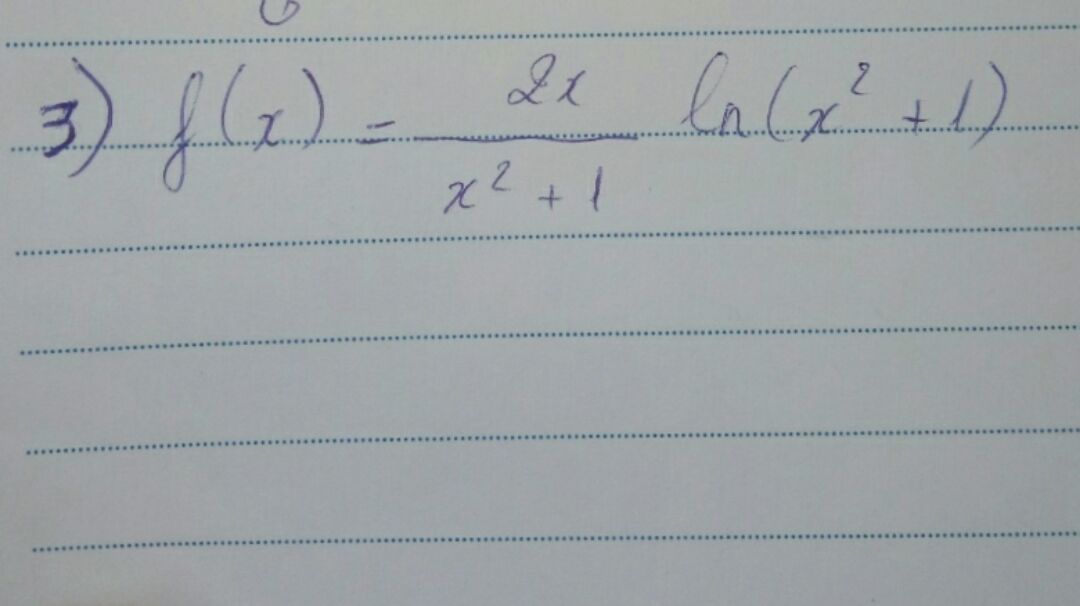 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Tính tích phân
bởi Trần Cúc
 17/03/2020
17/03/2020
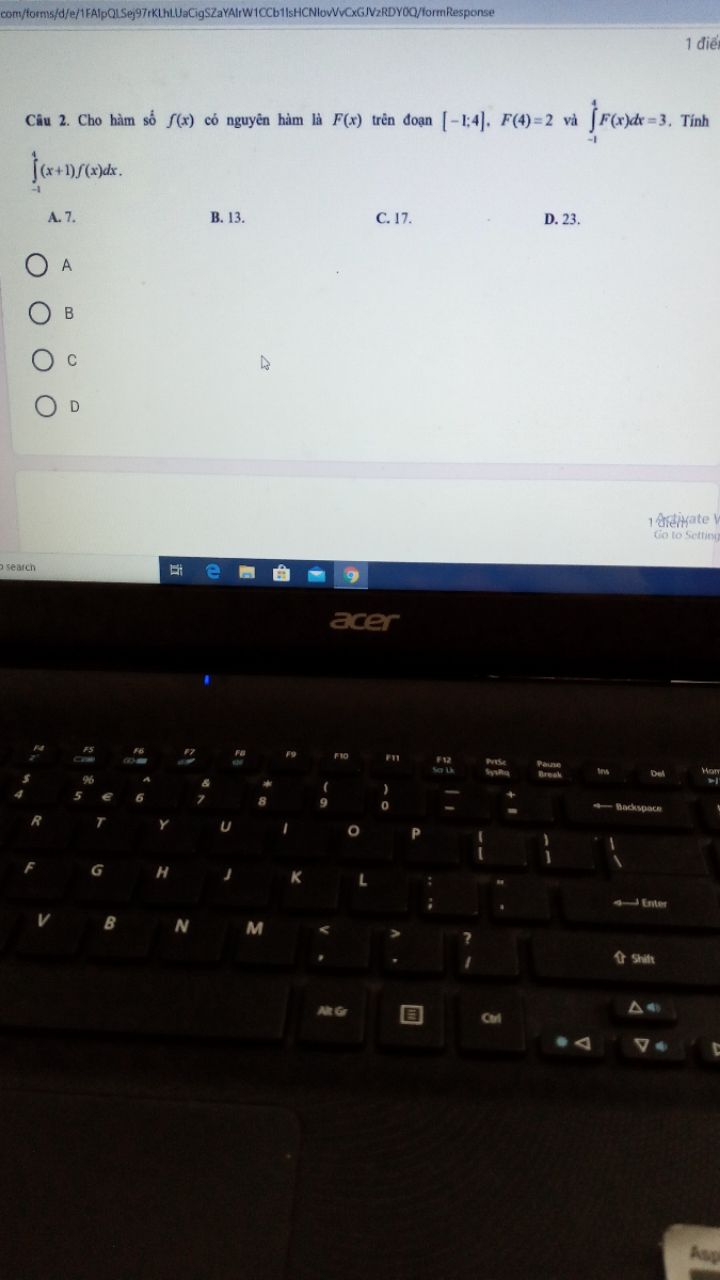 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Trắc nghiệm nguyên hàm, tích phân
bởi Xuân Thảo
 17/03/2020
Sao ạ??
17/03/2020
Sao ạ?? Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm nguyên hàm
bởi Đặng Phương Nam
 17/03/2020
Nguyên hàm
17/03/2020
Nguyên hàm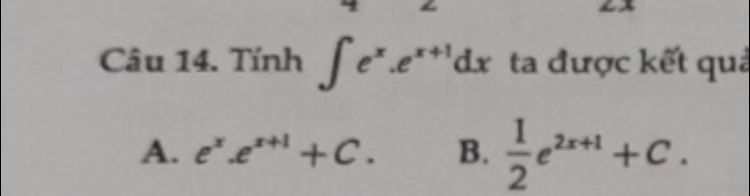 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tính nguyên hàm
bởi Lý Chí Phàm
 16/03/2020
Giúp mik vs mai mik nộp r :<<<
16/03/2020
Giúp mik vs mai mik nộp r :<<<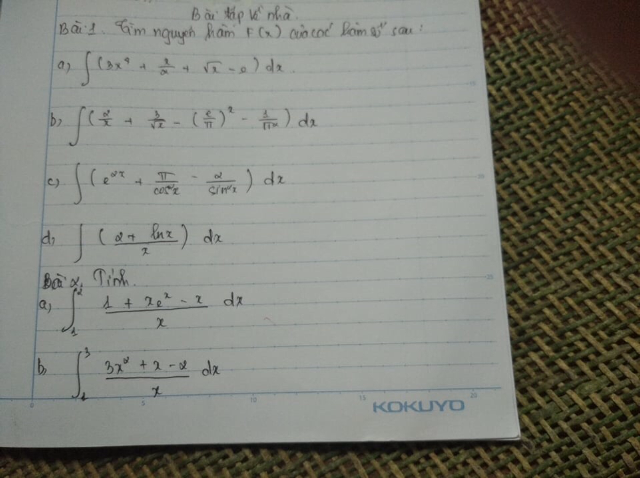 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Giải nguyên hàm
bởi Chủ Dếnh
 15/03/2020
Mấy bạn giúp mình giải bài này với
15/03/2020
Mấy bạn giúp mình giải bài này với Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm (x^3+3x^2+x)*e mũ (x^2+x-2)
bởi Lê Châu Thúy Vy
 13/03/2020
13/03/2020
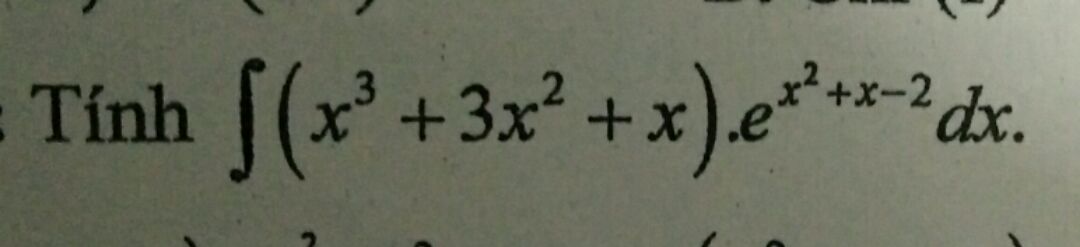 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính nguyên hàm x/(x^3-1)
bởi Lê Huỳnh Tuyết My
 13/03/2020
13/03/2020
Helpp mee pls
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3.6 trang 164 SBT Toán 12
Bài tập 3.7 trang 164 SBT Toán 12
Bài tập 3.9 trang 165 SBT Toán 12
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.11 trang 165 SBT Toán 12
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC





