Giải bài 3.12 tr 165 SBT Toán 12
\(\mathop \smallint \nolimits x{e^{2x}}dx\) bằng
A. \(\mathop \smallint \nolimits \frac{{{e^{2x}}(x - 2)}}{2} + C\)
B. \(\mathop \smallint \nolimits \frac{{{e^{2x}} + 1}}{2} + C\)
C . \(\mathop \smallint \nolimits \frac{{{e^{2x}}(x - 1)}}{2} + C\)
D . \(\mathop \smallint \nolimits \frac{{{e^{2x}}(2x - 1)}}{4} + C\)
Hướng dẫn giải chi tiết
Đặt \(\left\{ \begin{array}{l}
u = x\\
dv = {e^{2x}}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = \frac{1}{2}{e^{2x}}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
\mathop \smallint \nolimits x{e^{2x}}dx = \frac{1}{2}x{e^{2x}} - \frac{1}{2}\mathop \smallint \nolimits {e^{2x}}dx = \frac{1}{2}x{e^{2x}} - \frac{1}{4}{e^{2x}} + C\\
= \frac{{{e^{2x}}(2x - 1)}}{4} + C
\end{array}\)
Chọn đáp án D
-- Mod Toán 12 HỌC247
-


Họ nguyên hàm của hàm số y=x/x+1 là?
bởi Nguyễn Thị Nhi
 10/02/2020
10/02/2020
Cau 1:Họ nguyên hàm của hs Y=x/x+1 là:
Câu 2: cho hs f(x) thỏa f'(x)=sin(3x-1)+3, f(1/3)=2/3. Khi đó f(π) gần với số nào nhất
Câu 3: tìm a,b,c để F(x)=(ax^2+bx+c)×e^x là một nguyên hàm của f(x)=(x^2+4x+5)×e^x
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm x(x^2+1)^2
bởi Đoàn Thái Bảo
 10/02/2020
Tìm nguyên hàm
10/02/2020
Tìm nguyên hàm Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm f(x) = 1/e^x
bởi Nhi Uyên
 09/02/2020
f(x) = 1/e^xTheo dõi (0) 0 Trả lời
09/02/2020
f(x) = 1/e^xTheo dõi (0) 0 Trả lời -


Tính f(1/2) biết hàm số f(x) > 0 với mọi x thuộc R và có đạo hàm f'(x) thỏa mãn hệ thức
bởi Nguyễn Hoàng Việt
 09/02/2020
09/02/2020
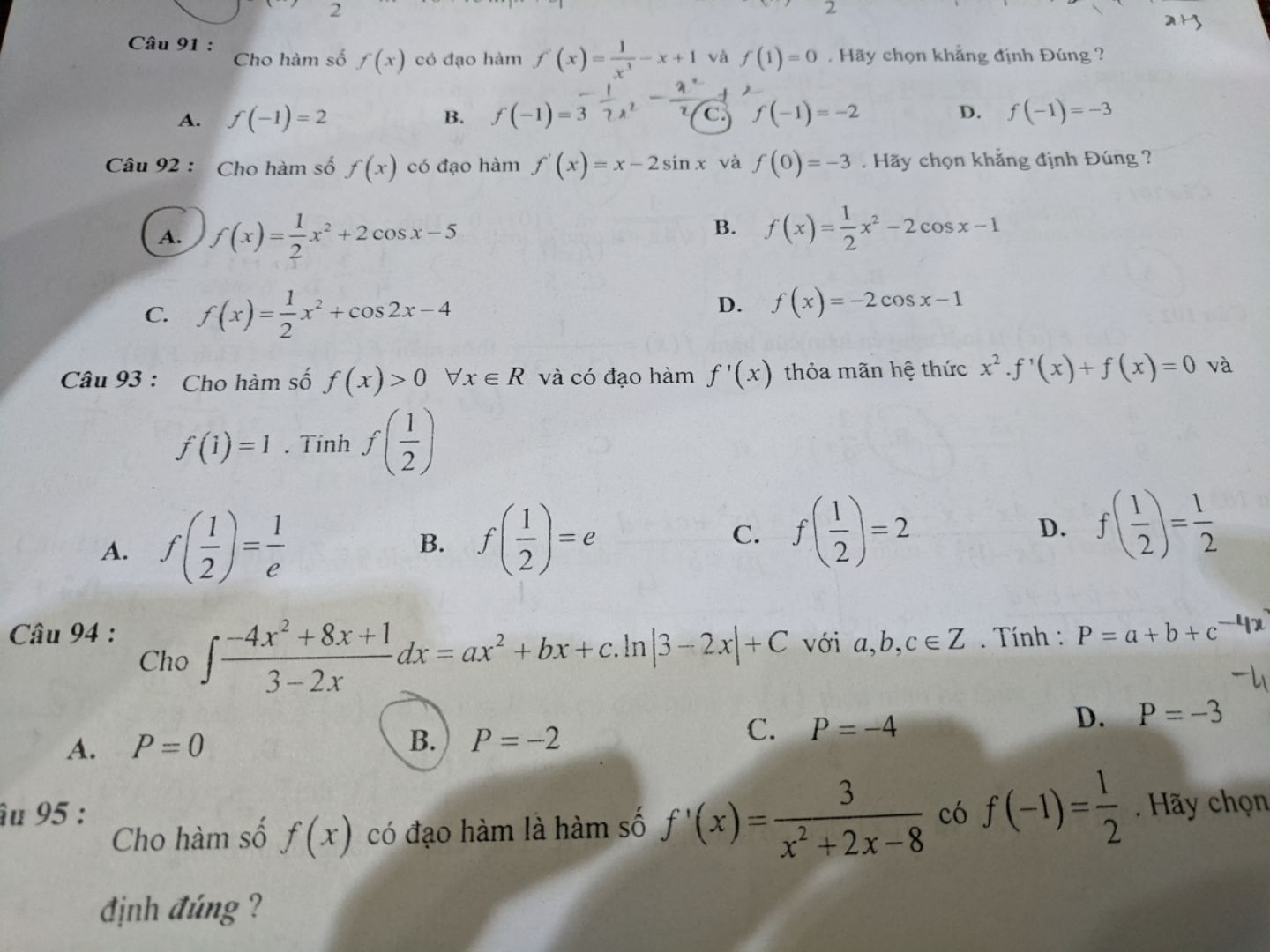 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm họ nguyên hàm của f(x)=sin^4x.cosx
bởi Vy Tran
 09/02/2020
09/02/2020
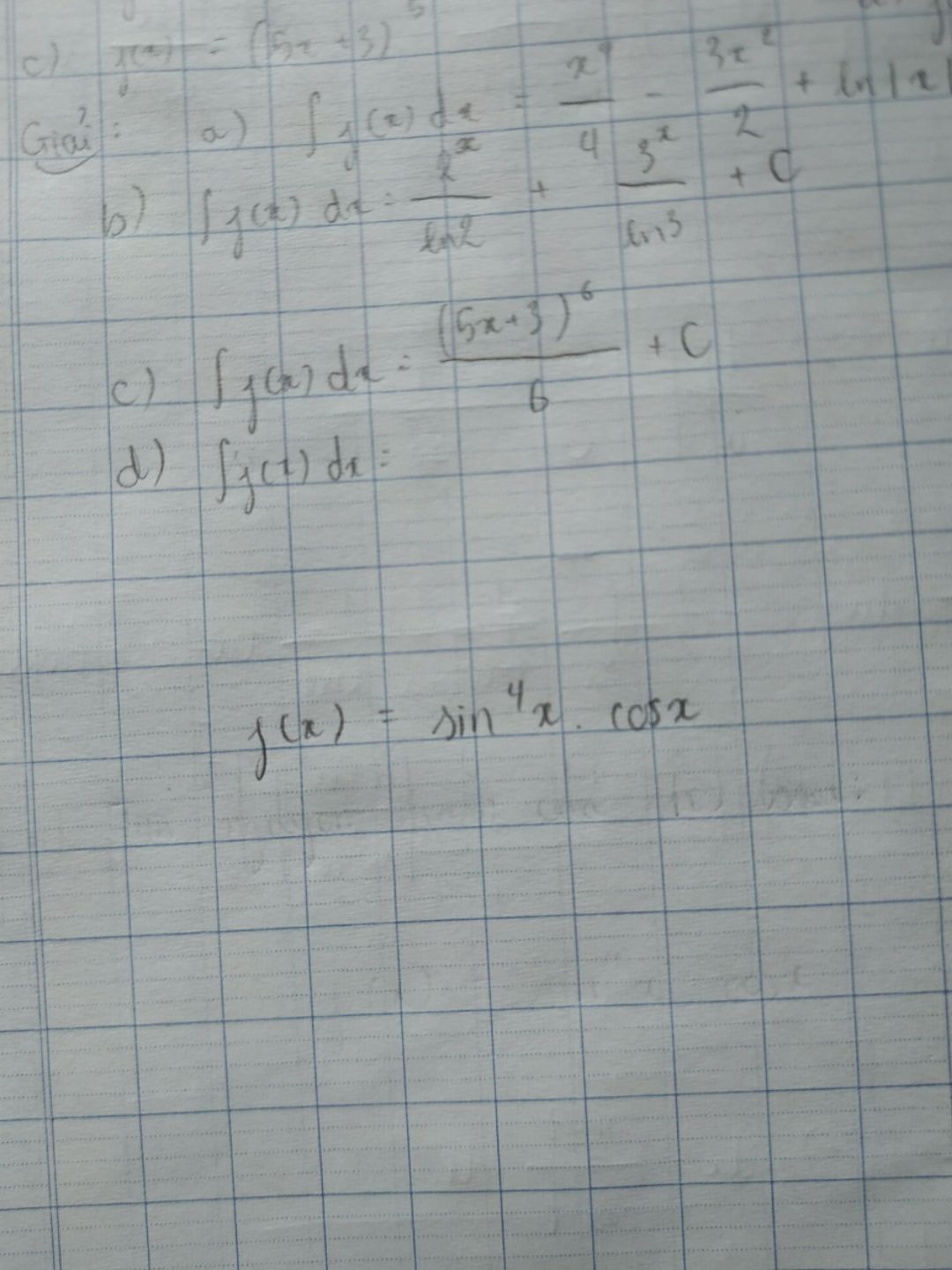 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm F(x) của f(x) biết F(pi/4)=1/2, F(pi/6)=0
bởi Trà Mi
 09/02/2020
Giúp em câu 174 ạ
09/02/2020
Giúp em câu 174 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nguyên hàm (x-2)^10/(x+1)^12 dx bằng?
bởi Nguyễn Hoàng Việt
 08/02/2020
08/02/2020
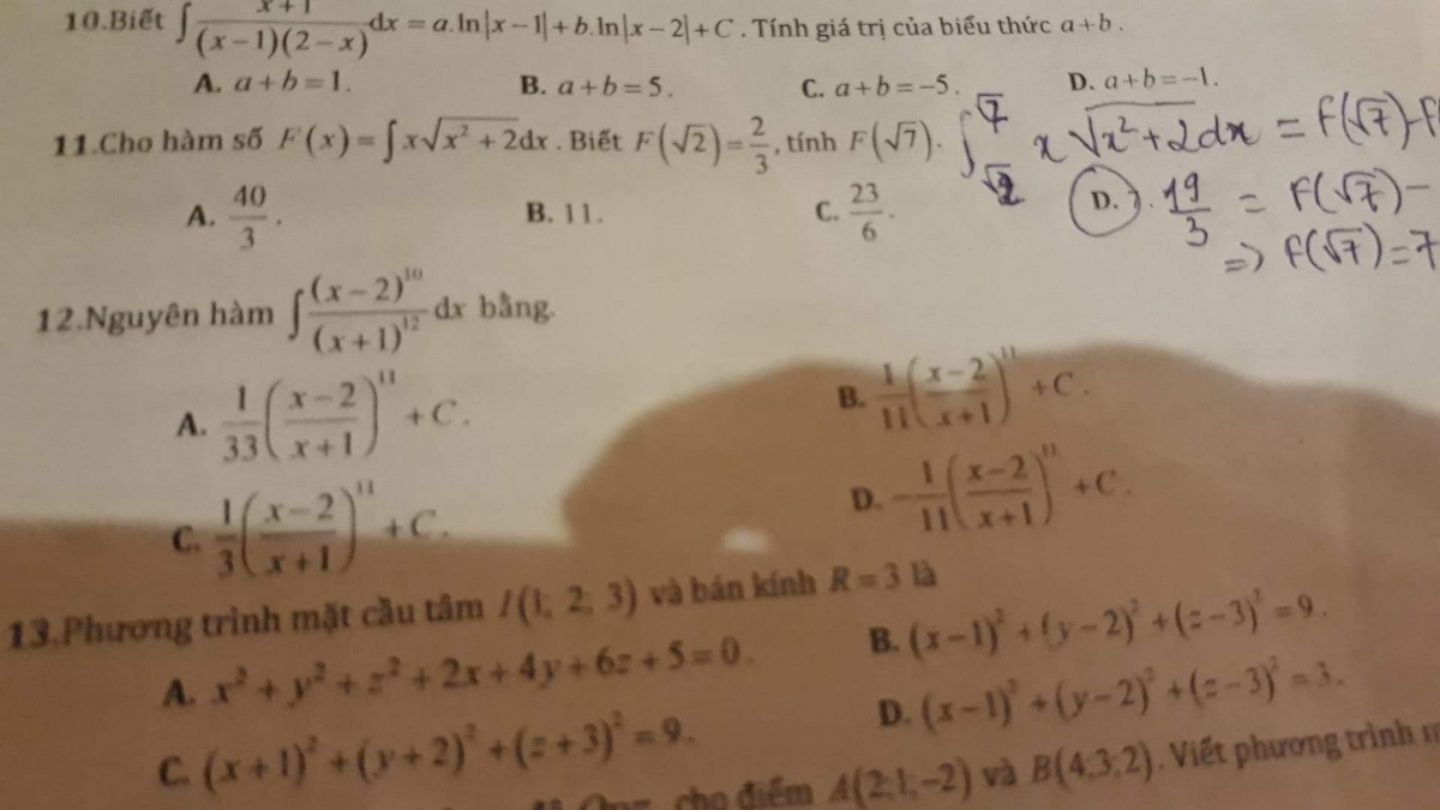 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tính F(x)=nguyên hàm 2x(3x-2)^6dx
bởi Baka Cun
 08/02/2020
08/02/2020
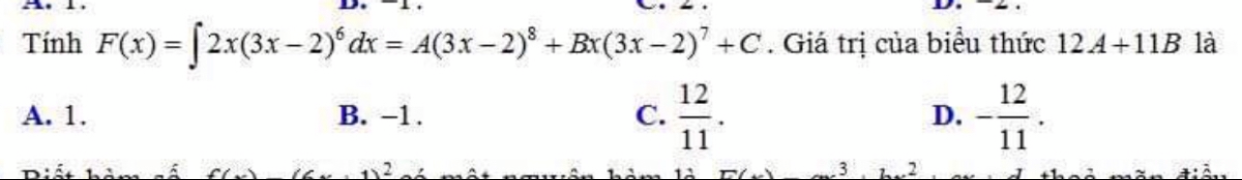 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính nguyên hàm f(x)=x^5 căn(x^3+1)
bởi Nguyễn Nhật
 08/02/2020
Giúp em câu 2 với ạ
08/02/2020
Giúp em câu 2 với ạ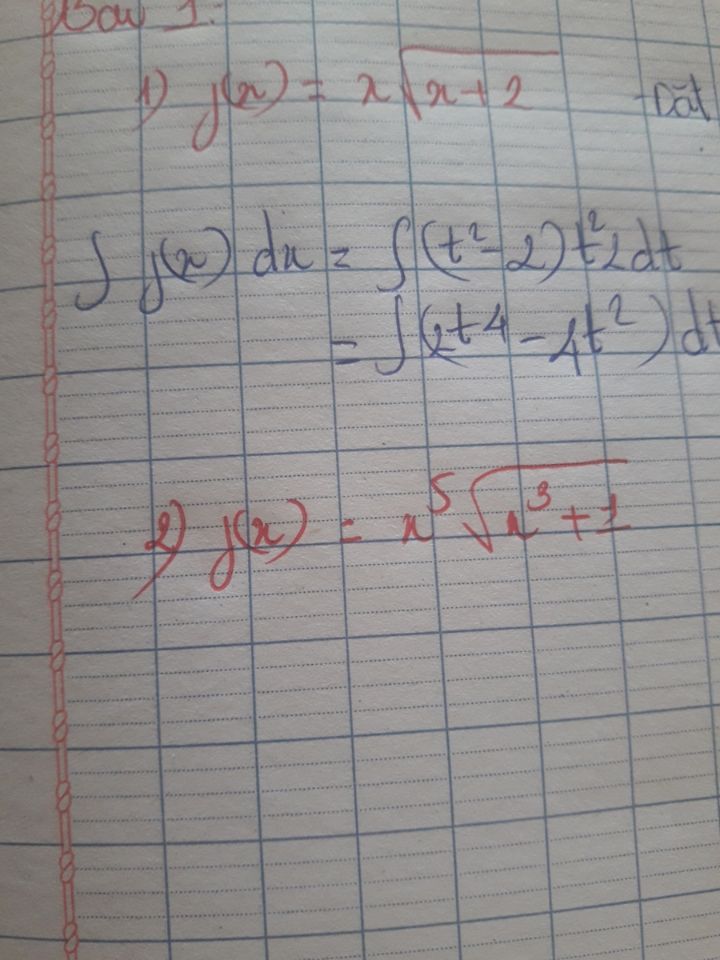 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của (1/(x^2)).cos(2/x)
bởi Nhật Hạ
 08/02/2020
Tìm nguyên hàm của (1/(x^2)).cos(2/x)
08/02/2020
Tìm nguyên hàm của (1/(x^2)).cos(2/x) Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -

 Câu 9 ạ
Câu 9 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của 1/cos^2 x+sin2x
bởi Khang Nguyen
 08/02/2020
Nguen ham 1/cos^2 x sin2xTheo dõi (0) 0 Trả lời
08/02/2020
Nguen ham 1/cos^2 x sin2xTheo dõi (0) 0 Trả lời -


Tính nguyên hàm của e^cosx.sinx dx
bởi Nguyen Nhật Lệ
 07/02/2020
Tính nguyên hàm của e mũ cosin x nhân với sin x dxTheo dõi (0) 0 Trả lời
07/02/2020
Tính nguyên hàm của e mũ cosin x nhân với sin x dxTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của 2x(1+3x^3)
bởi My Hoàng
 07/02/2020
Trả lời giúp em câu 1 với ạ
07/02/2020
Trả lời giúp em câu 1 với ạ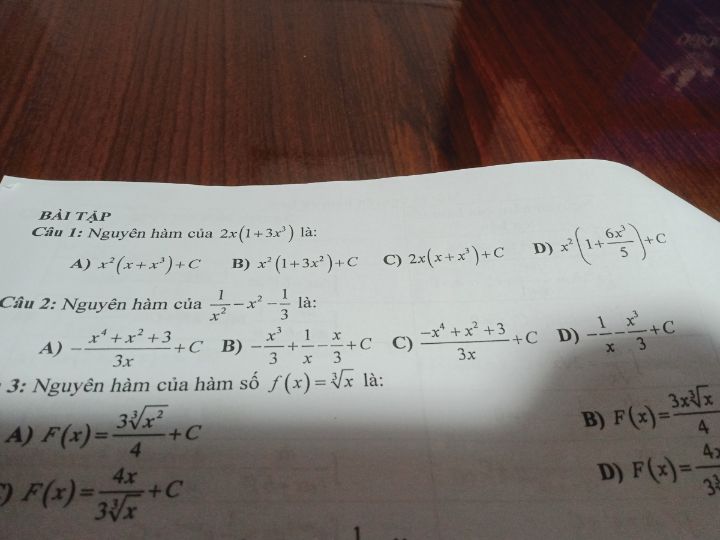 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nguyên hàm của hàm số y=x.e^ 2x
bởi Yến Moon
 06/02/2020
06/02/2020
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Tìm nguyên hàn F(-2) biết F(x) đi qua điểm M (2;10) và f(x) = x3 3x -2
Tìm nguyên hàn F(-2) biết F(x) đi qua điểm M (2;10) và f(x) = x3 3x -2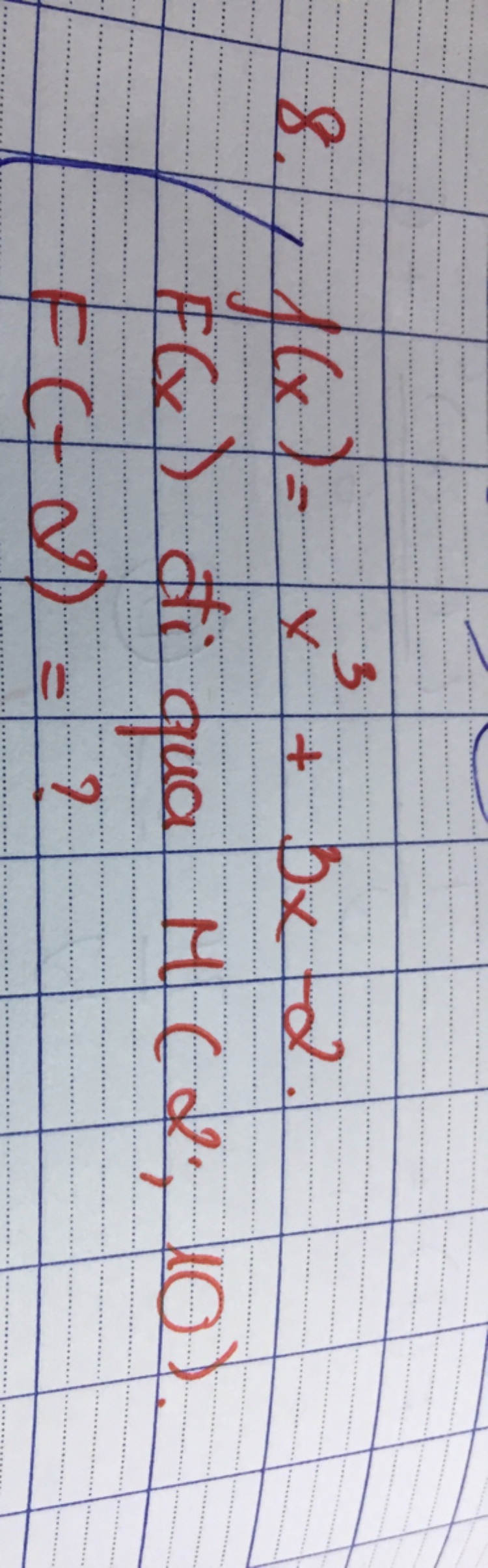 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của 3/x(x^3+4)dx
bởi Phan Thị Kim Ngân
 05/02/2020
!!!
05/02/2020
!!!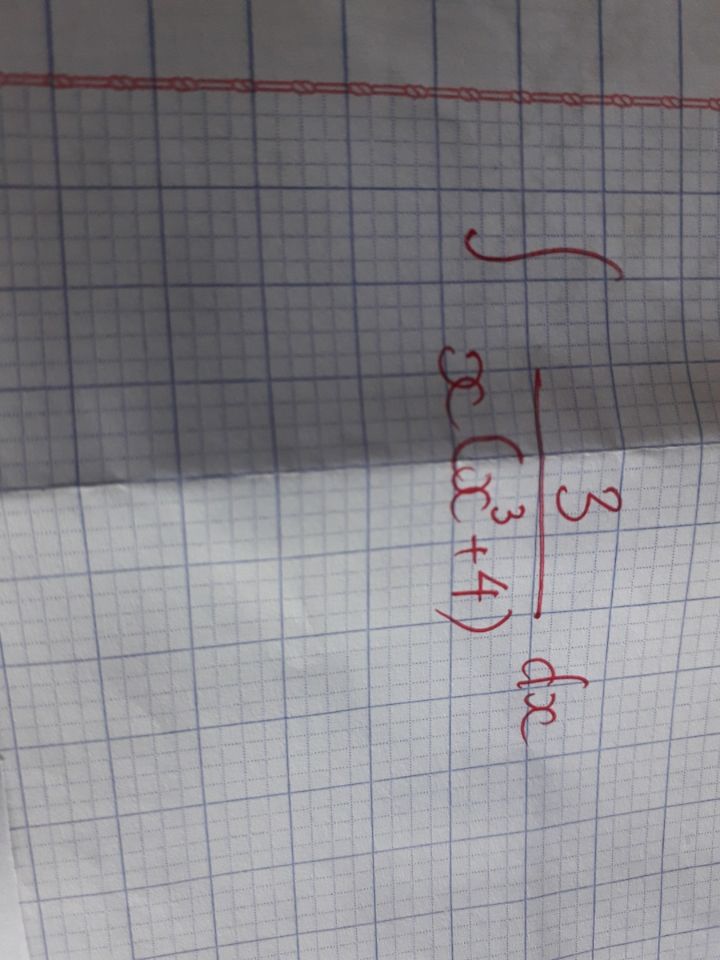 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Help me
Help me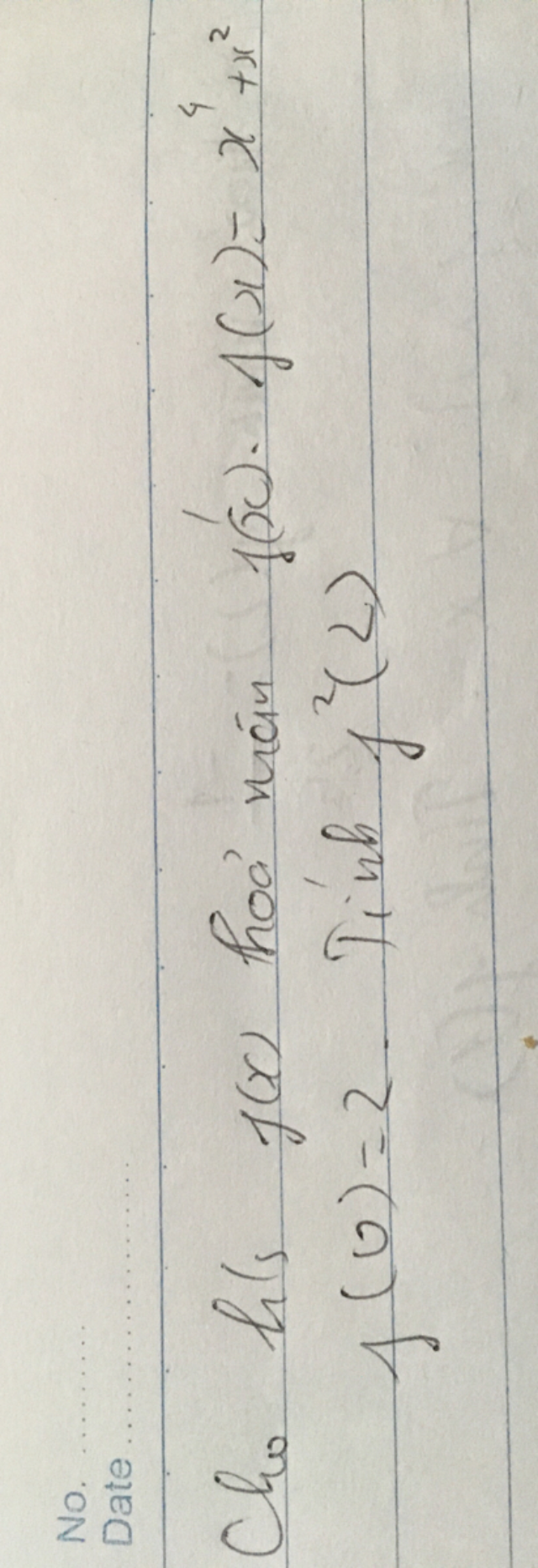 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính nguyên hàm của 1/e^x+1
bởi Lê Yến
 04/02/2020
K có
04/02/2020
K có Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nguyên hàm của 5^xlnx?
bởi Nguyễn Khoa
 02/02/2020
5 mũ x lnxTheo dõi (0) 1 Trả lời
02/02/2020
5 mũ x lnxTheo dõi (0) 1 Trả lời -


Tìm nguyên hàm của y=2lnx/x
bởi Thu Thơm
 02/02/2020
Tìm nguyên hàm của y=2lnx/xTheo dõi (0) 1 Trả lời
02/02/2020
Tìm nguyên hàm của y=2lnx/xTheo dõi (0) 1 Trả lời -


Tìm nguyên hàm của y=2lnx/x
bởi Thu Thơm
 02/02/2020
Tìm nguyên hàm của y=2lnx/xTheo dõi (0) 0 Trả lời
02/02/2020
Tìm nguyên hàm của y=2lnx/xTheo dõi (0) 0 Trả lời -


Tính nguyên hàm của 3^(1-2x).2^3xdx
bởi Phương Di
 02/02/2020
Tính nguyên hàm
02/02/2020
Tính nguyên hàm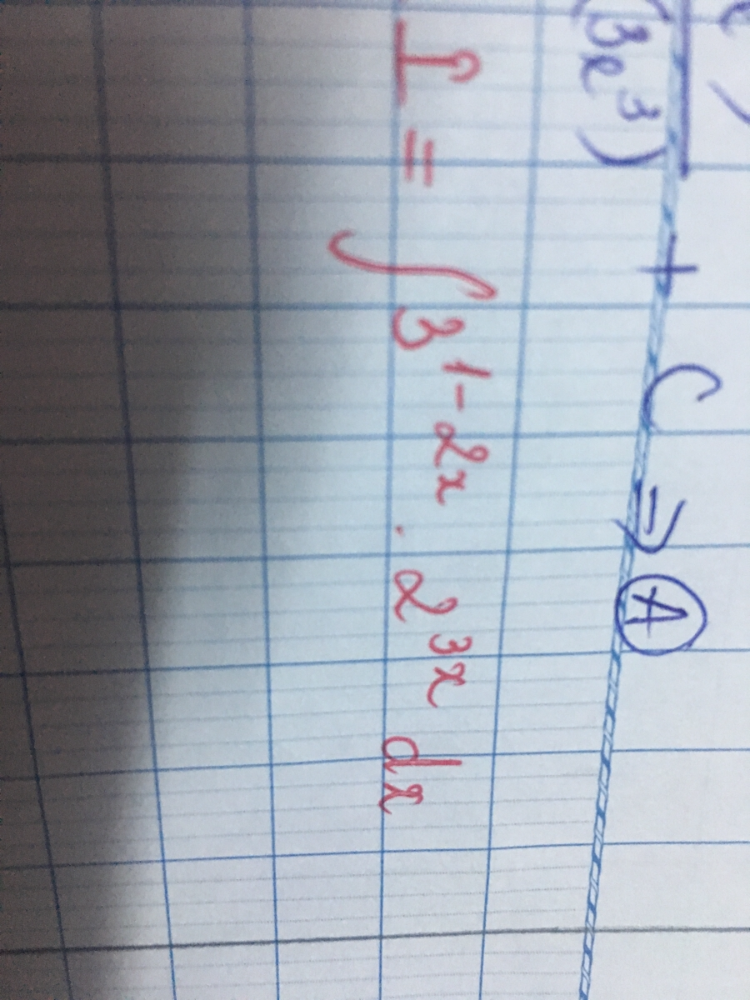 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.11 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC





