Giải bài 3.14 tr 166 SBT Toán 12
\(\mathop \smallint \nolimits x\ln (x + 1)dx\) bằng:
A. \(\left( {\frac{{{x^2}}}{2} - 1} \right)ln(x + 1) + \frac{1}{4}{(x - 1)^2} + C\)
B. \(\left( {\frac{{{x^2}}}{2} - 1} \right)\ln (x + 1) - \frac{1}{2}{(x - 1)^2} + C\)
C. \(\left( {\frac{{{x^2}}}{2} - \frac{1}{2}} \right)\ln (x + 1) - \frac{1}{4}{(x - 1)^2} + C\)
D. \(\left( {\frac{{{x^2}}}{2} + 1} \right)\ln (x + 1) - \frac{1}{4}{(x - 1)^2} + C\)
Hướng dẫn giải chi tiết
Đặt \(\left\{ \begin{array}{l}
u = ln\left( {x + 1} \right)\\
dv = xdx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = \frac{{dx}}{{x + 1}}\\
v = \frac{1}{2}{x^2}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
\int {xln(x + 1)dx} = \frac{1}{2}{x^2}ln(x + 1) - \frac{1}{2}\int {\frac{{{x^2}}}{{x + 1}}} dx\\
= \frac{1}{2}{x^2}ln(x + 1) - \frac{1}{2}\int {\left( {x - 1 + \frac{1}{{x + 1}}dx} \right)} \\
= \frac{1}{2}{x^2}\ln \left( {x + 1} \right) - \frac{1}{2}\left( {\frac{{{x^2}}}{2} - x + \ln \left| {x + 1} \right|} \right) + C\\
= \left( {\frac{{{x^2}}}{2} - \frac{1}{2}} \right)\ln \left( {x + 1} \right) - \frac{{{x^2}}}{4} + \frac{x}{2} + C\\
= \left( {\frac{{{x^2}}}{2} - \frac{1}{2}} \right)\ln \left( {x + 1} \right) - \frac{1}{4}{\left( {x - 1} \right)^2} + C
\end{array}\)
Chọn đáp án C.
-- Mod Toán 12 HỌC247
-


Tìm nguyên hàm của f(x)= 1/x^2 × cos2/xdx
bởi Nguyễn Diễm Quỳnh
 17/01/2020
Cho em hỏi bài này vớiTheo dõi (0) 0 Trả lời
17/01/2020
Cho em hỏi bài này vớiTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của ln(sinx)/cos^2x dx
bởi nguyenphuongthao
 16/01/2020
Giải giúp e bài 2 ý 10 ạ,e cảm ơn!!!
16/01/2020
Giải giúp e bài 2 ý 10 ạ,e cảm ơn!!!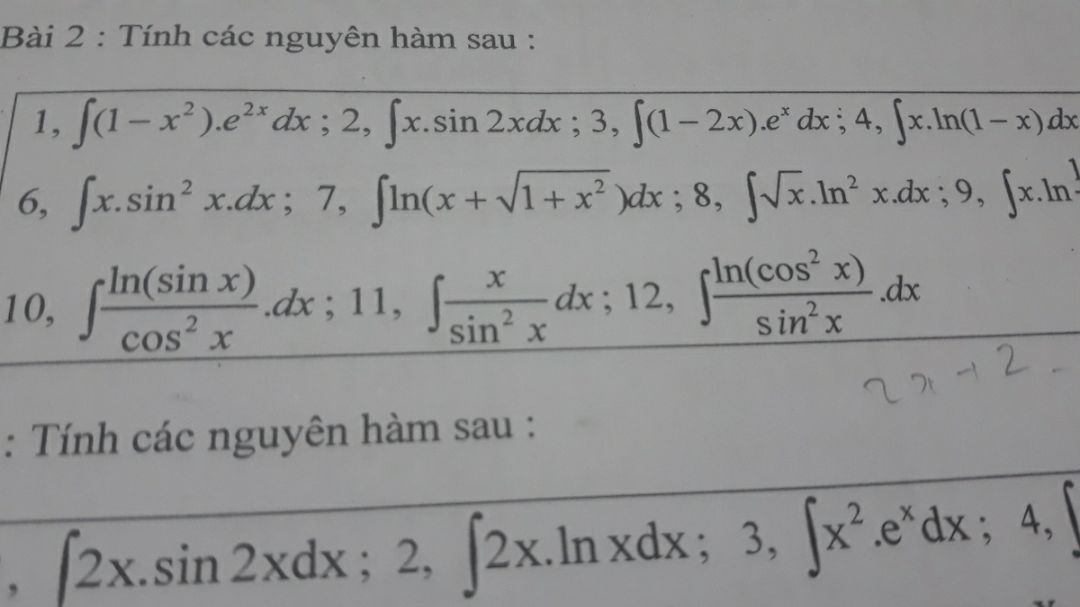 Theo dõi (2) 2 Trả lời
Theo dõi (2) 2 Trả lời -


Tìm nguyên hàm x/(cos(x))^2
bởi Nguyên Lê
 16/01/2020
Giúp vs mng oiTheo dõi (0) 4 Trả lời
16/01/2020
Giúp vs mng oiTheo dõi (0) 4 Trả lời -


Tìm nguyên hàm (1-x)^9dx
bởi Giang Nguyễn
 15/01/2020
15/01/2020
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tìm nguyên hàm của (1/e^x+ 4)
bởi Hoàng Vy
 14/01/2020
Mng giải dùm em câu này với ạTheo dõi (0) 0 Trả lời
14/01/2020
Mng giải dùm em câu này với ạTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của hàm số f'(x)e^2x
bởi Phương Uyên
 13/01/2020
cho f(x)=(x-1)e^x là một nguyên hàm của hàm số f(x)e^2x. tìm nguyên hàm của hàm số f'(x)e^2xTheo dõi (0) 1 Trả lời
13/01/2020
cho f(x)=(x-1)e^x là một nguyên hàm của hàm số f(x)e^2x. tìm nguyên hàm của hàm số f'(x)e^2xTheo dõi (0) 1 Trả lời -


Tính f(0)+f(-2)+f(4) biết f(-3)+f(3)=0
bởi Ngân Lê Thanh
 13/01/2020
13/01/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm nguyên hàm của x/cos^2x
bởi Quân Phan
 13/01/2020
Nguyên hàm của x/cos^2xTheo dõi (0) 0 Trả lời
13/01/2020
Nguyên hàm của x/cos^2xTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của ln2x
bởi Lê Văn Phi Trúc
 12/01/2020
Nguyên hàm của ln2xTheo dõi (0) 3 Trả lời
12/01/2020
Nguyên hàm của ln2xTheo dõi (0) 3 Trả lời -


Tìm nguyên hàm 2x+3/2x^2-x-1
bởi Thanh Đức
 12/01/2020
Toán 12 nguyên hàmTheo dõi (0) 0 Trả lời
12/01/2020
Toán 12 nguyên hàmTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của ln^3x/xdx
bởi Ngọc Hương
 12/01/2020
12/01/2020
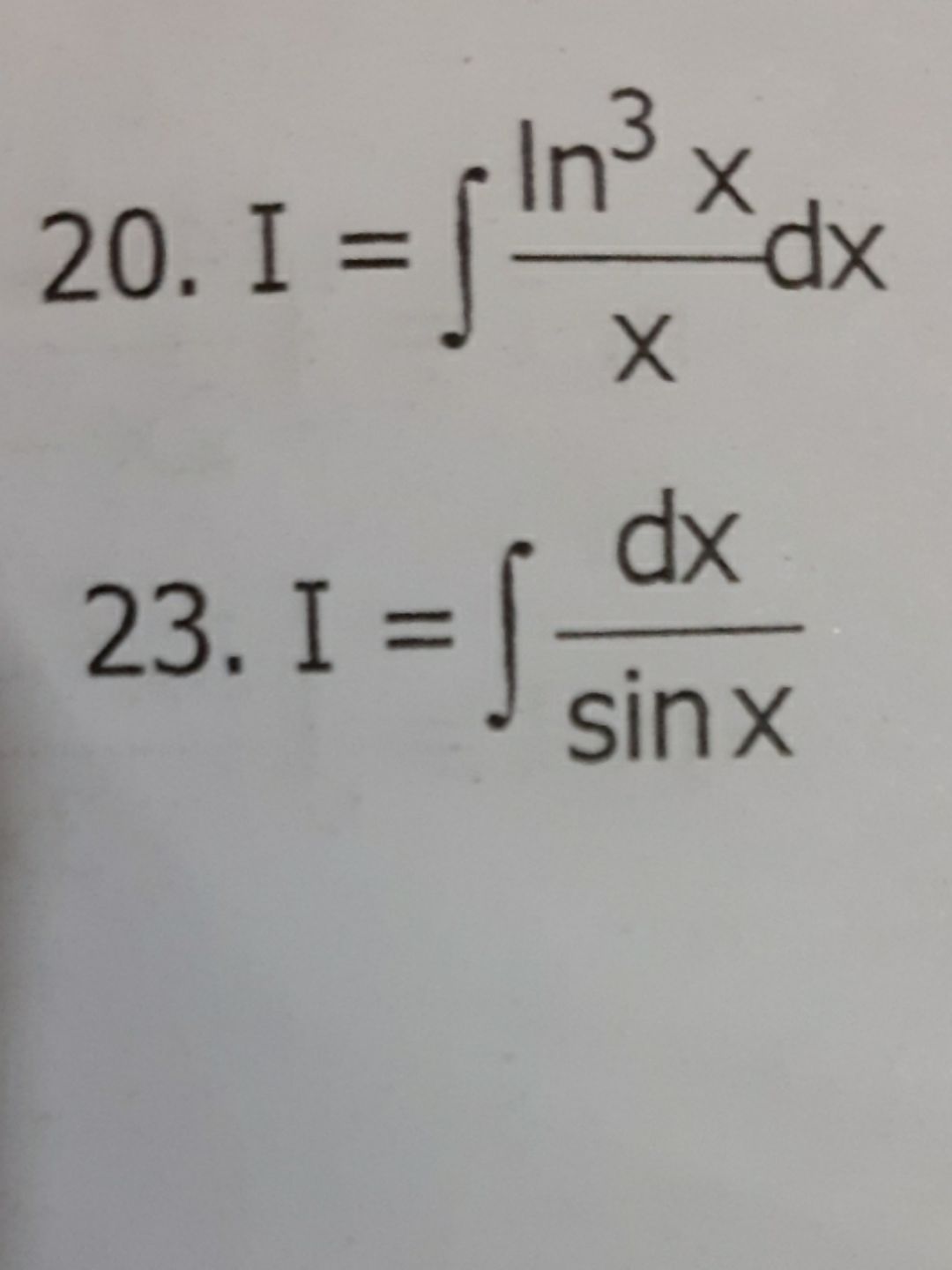 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của 1/ (cosx)^2+ sin2x
bởi Huỳnh Lan VI
 12/01/2020
12/01/2020
Nguyên hàm của 1/ (cosx)^2+ sin2x
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của e^x/e^x.căn(e^x-1)dx
bởi Vũ T. Hải Yến
 12/01/2020
Ý b ạ
12/01/2020
Ý b ạ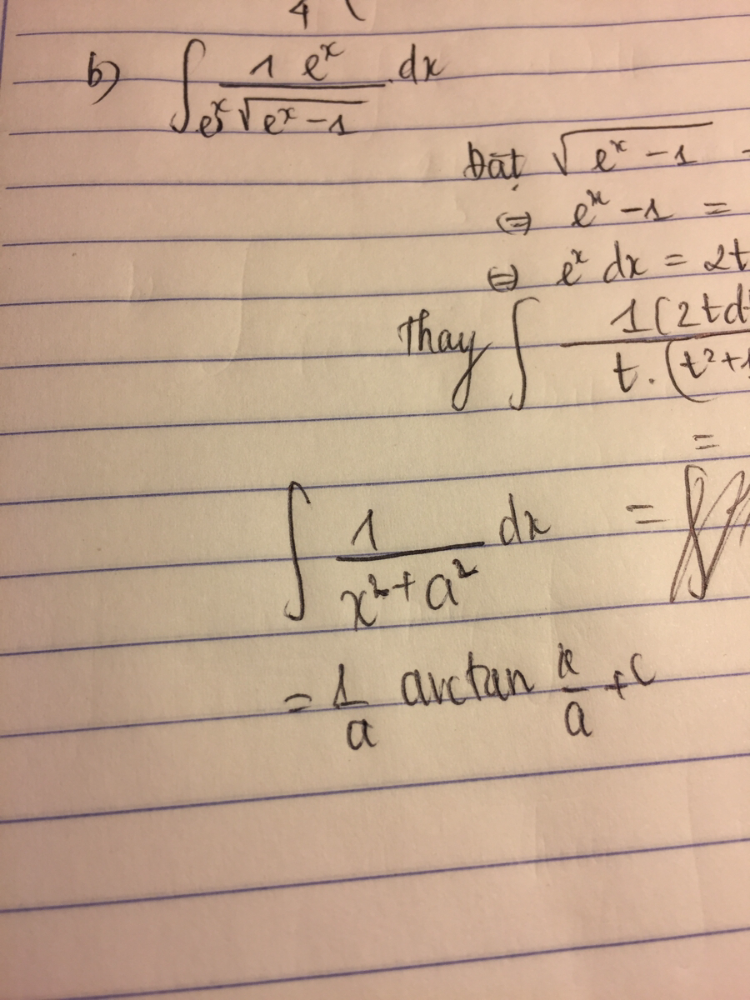 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm nnguyên hàm xlnx^2+1)/x^2+1
bởi Lê Văn Quân
 11/01/2020
(X*lnx^2 1)/x^2 1Theo dõi (0) 0 Trả lời
11/01/2020
(X*lnx^2 1)/x^2 1Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của hàm số (x+1)^3/(x^2+2x-3)
bởi Trường Đông
 11/01/2020
Tìm nguyên hàm của hsTheo dõi (0) 0 Trả lời
11/01/2020
Tìm nguyên hàm của hsTheo dõi (0) 0 Trả lời -


Nguyên hàm của tan^2 x?
bởi Phan Văn Hoàng
 10/01/2020
.............Theo dõi (0) 0 Trả lời
10/01/2020
.............Theo dõi (0) 0 Trả lời -


Nguyên hàm của (cos^4 x-sin^4 x)dx?
bởi Dong Dong
 10/01/2020
10/01/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Nguyên hàm e^x . ln(x) dx?
bởi Bùi Dương
 10/01/2020
10/01/2020
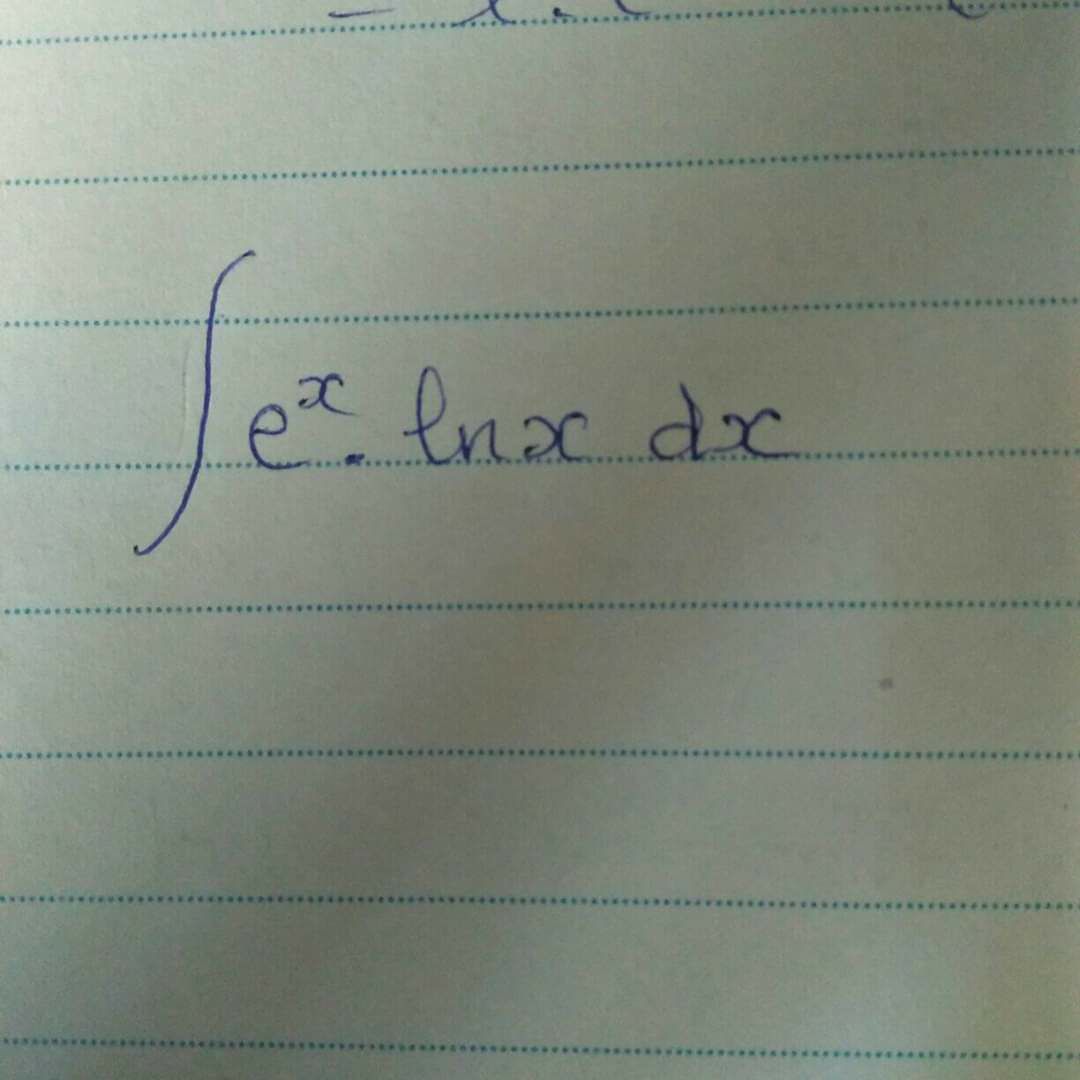 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của 3x^2.căn(x^3+1)dx
bởi Lê Liêm
 10/01/2020
10/01/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của x.lnxdx
bởi Tiến Nhật
 10/01/2020
Tính
10/01/2020
Tính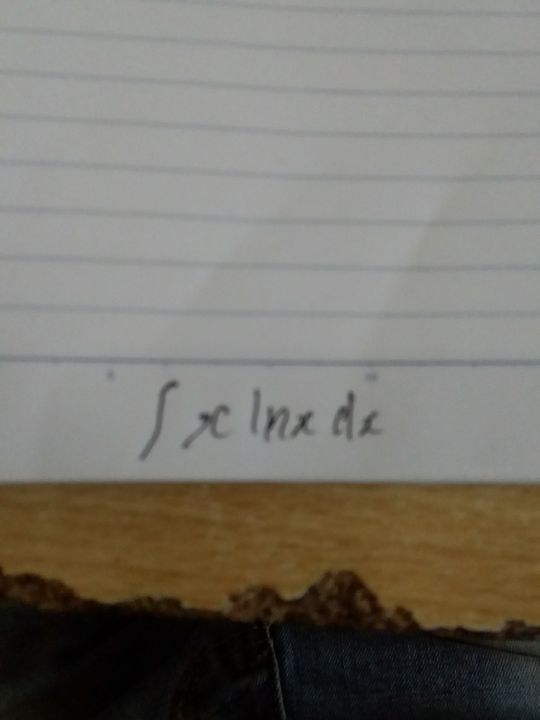 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm họ các nguyên hàm của hàm sô y=tan^3 x?
bởi Lan Anh
 10/01/2020
10/01/2020
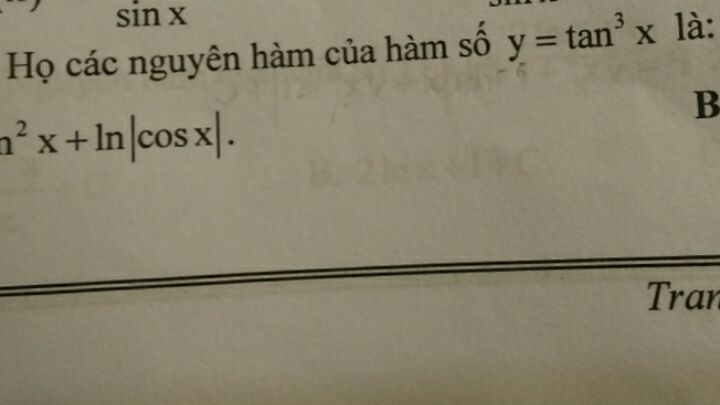 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm nnguyên hàm của hàm số f(x)=xcosx^2
bởi Nguyễn Doanh
 10/01/2020
Tìm nguyên hàmTheo dõi (0) 0 Trả lời
10/01/2020
Tìm nguyên hàmTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm x^3/căn(2-x^2)
bởi Như Yến
 09/01/2020
Tìm nguyên hàm x^3/√2-x^2Theo dõi (0) 2 Trả lời
09/01/2020
Tìm nguyên hàm x^3/√2-x^2Theo dõi (0) 2 Trả lời -


Nguyên hàm sin(3x-1)dx?
bởi Ng Phươngg Thảo
 09/01/2020
Câu trả lờiTheo dõi (0) 1 Trả lời
09/01/2020
Câu trả lờiTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC





