Bài tập 1 trang 141 SGK Toán 12 NC
Tìm nguyên hàm của các hàm số sau :
\(\begin{array}{l}
a)f\left( x \right) = 3{x^2} + \frac{x}{2}\\
b)f(x) = 2{x^3} - 5x + 7\\
c)f\left( x \right) = \frac{1}{{{x^2}}} - {x^2} - \frac{1}{3}\\
d)f(x) = {x^{ - \frac{1}{3}}}\\
e)f(x) = {10^{2x}}
\end{array}\)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\int {\left( {3{x^2} + \frac{x}{2}} \right)} dx\\
= 3\int {{x^2}dx} + \frac{1}{2}\int {xdx} \\
= {x^3} + \frac{{{x^2}}}{4} + C
\end{array}\)
b)
\(\begin{array}{l}
\int {\left( {2{x^3} - 5x + 7} \right)} dx\\
= 2\int {{x^3}dx} - 5\int {xdx} + 7\int {dx} \\
= \frac{{{x^4}}}{2} - \frac{{5{x^2}}}{4} + 7x + C
\end{array}\)
c)
\(\begin{array}{l}
\int {\left( {\frac{1}{{{x^2}}} - {x^2} - \frac{1}{3}} \right)} dx\\
= \int {{x^{ - 2}}dx} - \int {{x^2}dx} - \frac{1}{3}\int {dx} \\
= - \frac{1}{x} - \frac{{{x^3}}}{3} - \frac{x}{3} + C
\end{array}\)
d) \(\int {\left( {{x^{ - \frac{1}{3}}}} \right)} dx = \frac{{{x^{\frac{2}{3}}}}}{{\frac{2}{3}}} + C = \frac{3}{2}{x^{\frac{2}{3}}} + C\)
e) \(\int {{{10}^{2x}}} dx = \frac{{{{10}^{2x}}}}{{2.\ln 10}} + C\)
-- Mod Toán 12 HỌC247
-


Tìm nguyên hàm của e^(x^2+2)
bởi Ngoc Anhh
 01/01/2020
01/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của xsinx.cos2x
bởi Nguyễn Thu Hường
 01/01/2020
Tìm nguyên hàm của XsinXcos2X
01/01/2020
Tìm nguyên hàm của XsinXcos2X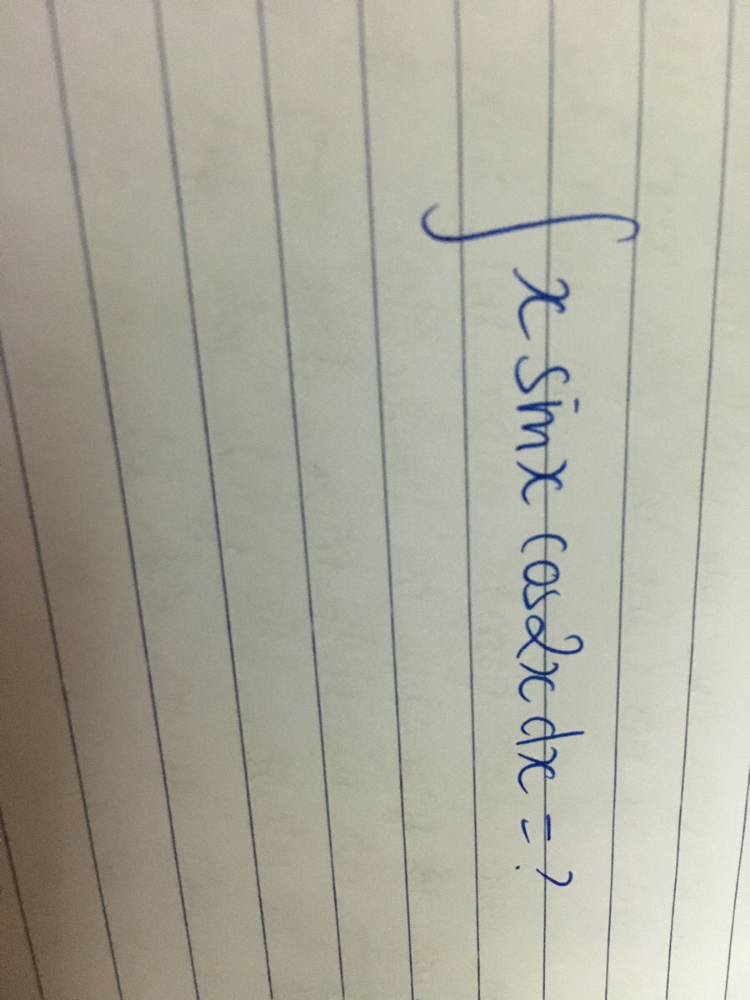 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm nguyên hàm của e^(x^2+2)
bởi Phàm Dương Chính
 31/12/2019
Tìm nguyên hàm của e^(x^2 2)Theo dõi (1) 1 Trả lời
31/12/2019
Tìm nguyên hàm của e^(x^2 2)Theo dõi (1) 1 Trả lời -


Tính nguyên hàm của hàm số y=3x^2+6x+1
bởi Hương Võ
 30/12/2019
Giải dùm em mấy câu em đánh dấu với ạ
30/12/2019
Giải dùm em mấy câu em đánh dấu với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm của 2 sin2xdx
bởi Nguyễn Quyên
 30/12/2019
30/12/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm đạo hàm của xlnx
bởi Nam Phạm Trần Phương
 30/12/2019
Đạo hàm của xlnxTheo dõi (0) 6 Trả lời
30/12/2019
Đạo hàm của xlnxTheo dõi (0) 6 Trả lời -


Lấy ví dụ nguyên hàm
bởi Ước Mơ Theo Đuổi
 30/12/2019
Nguyên hàmTheo dõi (0) 0 Trả lời
30/12/2019
Nguyên hàmTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm 1/1+e^xdx
bởi Nguyen Duy
 29/12/2019
nguyên hàm 1/1 e^xTheo dõi (0) 1 Trả lời
29/12/2019
nguyên hàm 1/1 e^xTheo dõi (0) 1 Trả lời -


Nguyên hàm của 1/e^x?
bởi An Le
 29/12/2019
Nguyên hàm của 1/e^xTheo dõi (0) 0 Trả lời
29/12/2019
Nguyên hàm của 1/e^xTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm sin(3x-1)
bởi Lê Thị Ngọc Trân
 29/12/2019
29/12/2019
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm (2x+1)^3
bởi Heo Pé
 29/12/2019
Nguyên hàmTheo dõi (0) 0 Trả lời
29/12/2019
Nguyên hàmTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của (2x-1)/(x^2-x)
bởi Minh Đức
 29/12/2019
29/12/2019
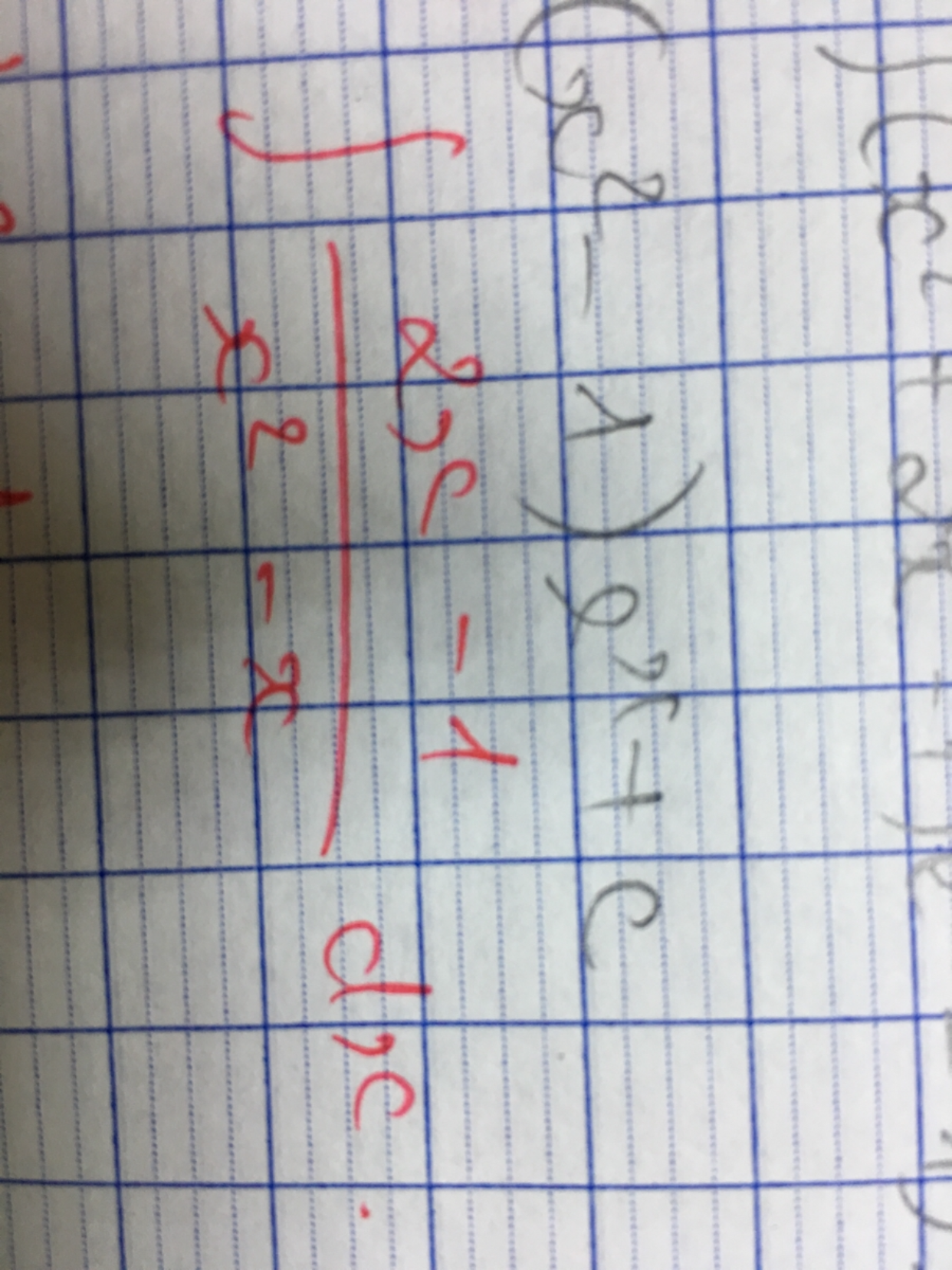 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm giá trị của tham số để nguyên hàm F(x) của hàm số f(x) thỏa điều kiện F(0)=1
bởi Liu Ly
 29/12/2019
29/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm I= dx/1+e^x
bởi Đặng Thảo Vân
 29/12/2019
Tìm
29/12/2019
Tìm Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


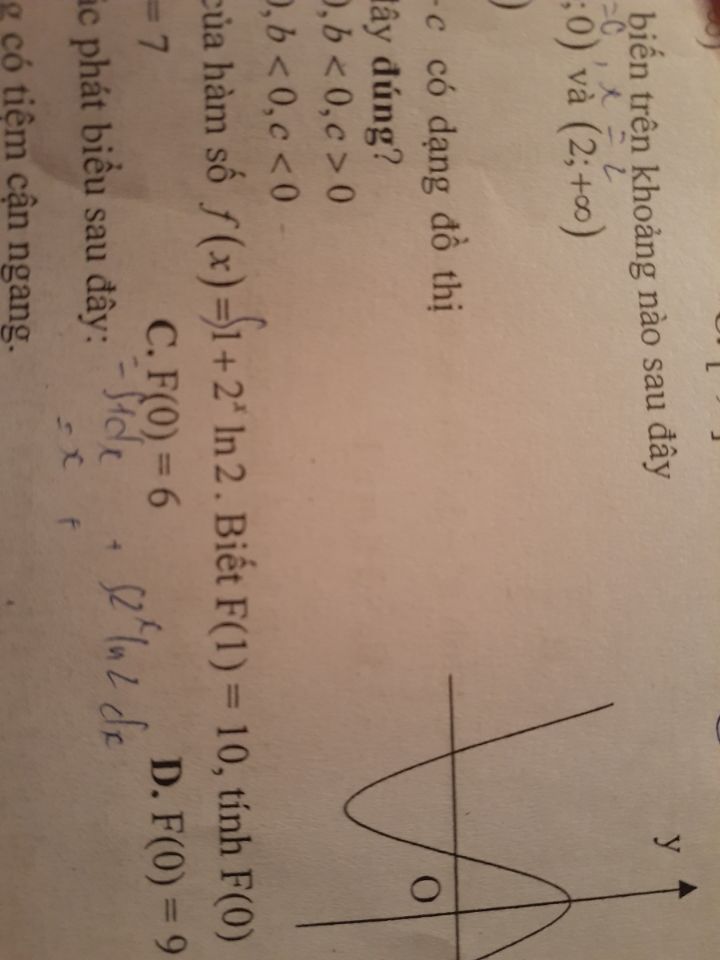 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Tìm nguyên hàm 4x(1+lnx)
bởi Hà Văn Đạt
 27/12/2019
4x(1 lnx) tìm nguyên hàm đấyTheo dõi (0) 2 Trả lời
27/12/2019
4x(1 lnx) tìm nguyên hàm đấyTheo dõi (0) 2 Trả lời -


Nguyên hàm của (2x-1)e^1/x
bởi Phạm Thị Mơ
 27/12/2019
Tính nguyên hàmTheo dõi (0) 6 Trả lời
27/12/2019
Tính nguyên hàmTheo dõi (0) 6 Trả lời -


Nguyên hàm (cosx)^3
bởi Sến Quỳnh
 27/12/2019
Tìm nguyên hàm
27/12/2019
Tìm nguyên hàm Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm nguyên hàm F(x) của f(x)=x căn(x^2+1)?
bởi Nguyễn Thị Su
 27/12/2019
Giúp e câu t
27/12/2019
Giúp e câu t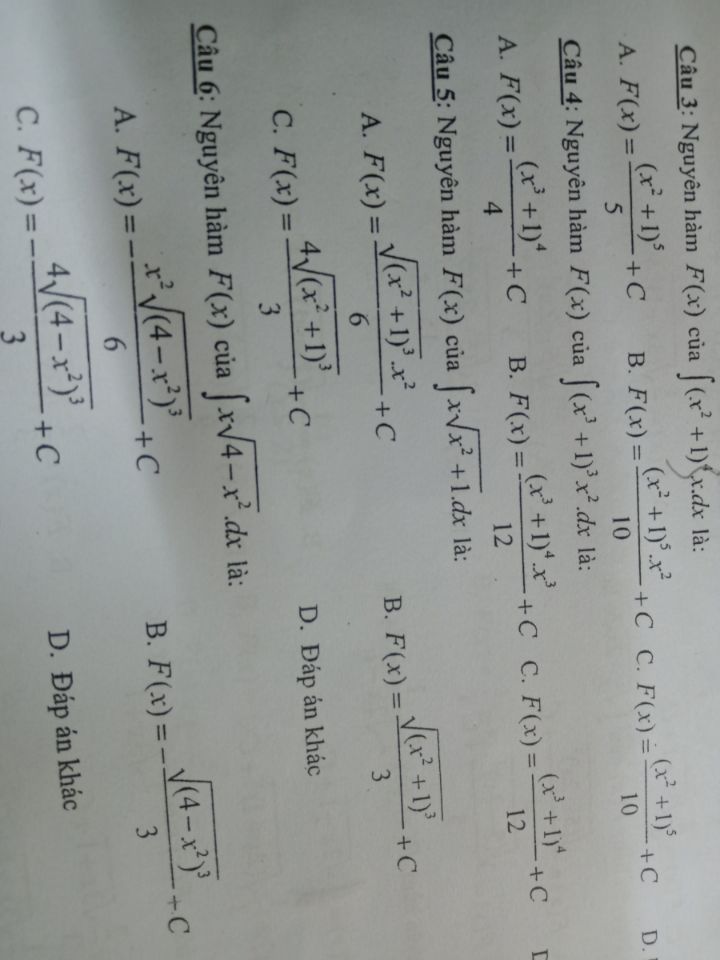 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Nguyên hàm của x căn x bình cộng 1?
bởi Nguyễn Thị Su
 27/12/2019
Giải bài tậpTheo dõi (0) 0 Trả lời
27/12/2019
Giải bài tậpTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm F(x)=2x^3+1/x(x^3-1)
bởi Đặng Nhung
 26/12/2019
F(x)=2x^3 1/x(x^3-1)
26/12/2019
F(x)=2x^3 1/x(x^3-1)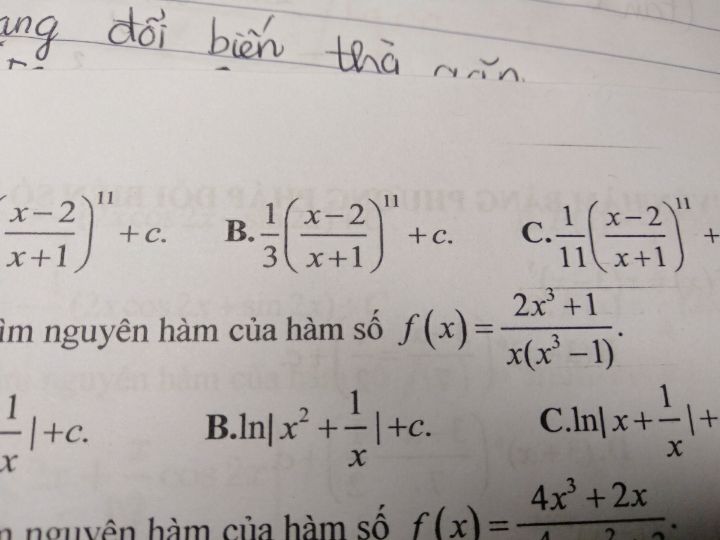 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính nguyên hàm của (x-2)/(x+1)dx
bởi Nguyễn Chinh
 26/12/2019
26/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của x.căn(x-1)dx
bởi Vương Ngọc Phượng
 25/12/2019
25/12/2019
 Theo dõi (2) 0 Trả lời
Theo dõi (2) 0 Trả lời -


Nguyên hàm ln(2x-3)?
bởi Nguyễn Thị Quỳnh Thương
 25/12/2019
Nguyên hàm ...Theo dõi (0) 0 Trả lời
25/12/2019
Nguyên hàm ...Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC





