Giải bài 3.11 tr 165 SBT Toán 12
Hãy chỉ ra kết quả sai khi tính \(\mathop \smallint \nolimits \sin x\cos xdx\)
A. \(\frac{{{{\sin }^2}x}}{2} + C\)
B. \( - \frac{{{{\cos }^2}x}}{2} + C\)
C. \(\frac{{ - \cos 2x}}{4} + C\)
D. \(\frac{{{{\cos }^2}x}}{2} + C\)
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\int {\sin x\cos xdx} = \int {\sin xd\left( {\sin x} \right)} \\
= \frac{{{{\sin }^2}x}}{2} + C\\
= - \frac{{{{\cos }^2}x}}{2} + C\\
= - \frac{1}{2}.\frac{{1 + \cos 2x}}{2} + C\\
= - \frac{{\cos 2x}}{4} + C
\end{array}\)
Đáp án D
-- Mod Toán 12 HỌC247
-


Nguyên hàm của x là gì?
bởi Mẫn Nhi
 14/02/2020
Nguyên hàm của x là gì?Theo dõi (0) 6 Trả lời
14/02/2020
Nguyên hàm của x là gì?Theo dõi (0) 6 Trả lời -


Nguyên hàm x.e^x^2+1?
bởi Mẫn Nhi
 14/02/2020
Nguyên hàm x.e^x^2 1Theo dõi (0) 1 Trả lời
14/02/2020
Nguyên hàm x.e^x^2 1Theo dõi (0) 1 Trả lời -


Nguyên hàm của f(x)=cos2x?
bởi Tuong Cmtr
 13/02/2020
13/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Nguyên hàm của (2x +1)/căn(x^2 +x +1)?
bởi Nguyễn Phương Nhất Vũ
 13/02/2020
Cách giải bài trênTheo dõi (0) 1 Trả lời
13/02/2020
Cách giải bài trênTheo dõi (0) 1 Trả lời -


Tìm nguyên hàm e^x sin^2xdx
bởi Đặngg Vănn Tú
 13/02/2020
giả nguyên hàmTheo dõi (0) 0 Trả lời
13/02/2020
giả nguyên hàmTheo dõi (0) 0 Trả lời -


Tìm nguyên hàm của xdx/(x+căn(x^2-1))
bởi Bin Lê
 13/02/2020
13/02/2020
 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tìm nguyên hàm của 4/(1+2x)dx
bởi Hươngg Tràa
 12/02/2020
12/02/2020
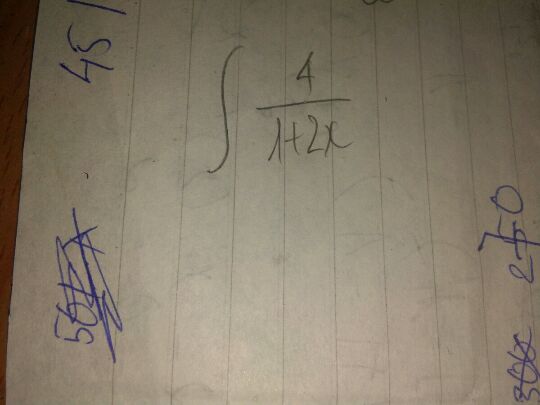 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -

 Câu 33 làm thế nào vậy
Câu 33 làm thế nào vậy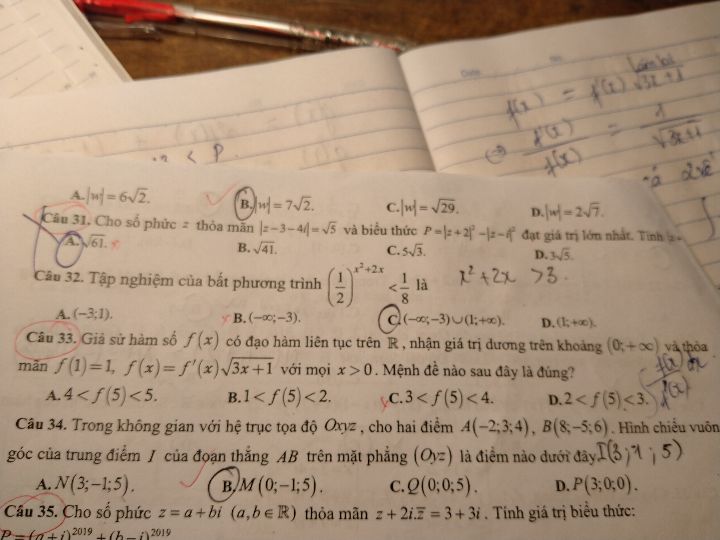 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Câu hỏi:Tìm một nguyên hàm F(x) của hàm số f(x)=2x(x2 1)^4,f(x)=2x(x2 1)^4, biết F(1)=6.
Câu hỏi:Tìm một nguyên hàm F(x) của hàm số f(x)=2x(x2 1)^4,f(x)=2x(x2 1)^4, biết F(1)=6. Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính tổng A=a+b+c biết f(x)=(ax^2+bx+c).e^-x là một nguyên hàm của hàm số g(x)=x(1-x).e^-x
bởi PhúC ĐạT
 12/02/2020
12/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


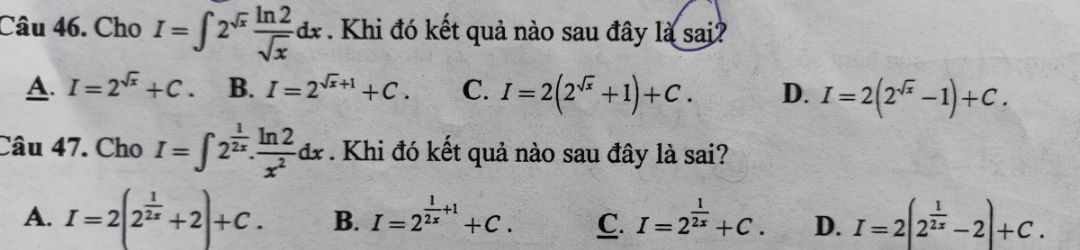 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của hàm số f(x) = 2x+1/x+e^3x
bởi Ly Nguyễn
 12/02/2020
Tìm nguyên hàm của hàm số f(x)
12/02/2020
Tìm nguyên hàm của hàm số f(x) Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của hàm số f(x)=cosx-cos3x
bởi Ngọc Ánh Nguyễn
 12/02/2020
12/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Nguyên hàm 1/cos^2(2x)dx?
bởi Hiền Lê Thu
 12/02/2020
Nguyên hàm 1/cos^2(2x)Theo dõi (0) 1 Trả lời
12/02/2020
Nguyên hàm 1/cos^2(2x)Theo dõi (0) 1 Trả lời -


Nguyên hàm của sinx^2.cosx.dx?
bởi Hà Tấn Được
 12/02/2020
Nguyên hàm của sinx^2.cosx.dxTheo dõi (0) 1 Trả lời
12/02/2020
Nguyên hàm của sinx^2.cosx.dxTheo dõi (0) 1 Trả lời -


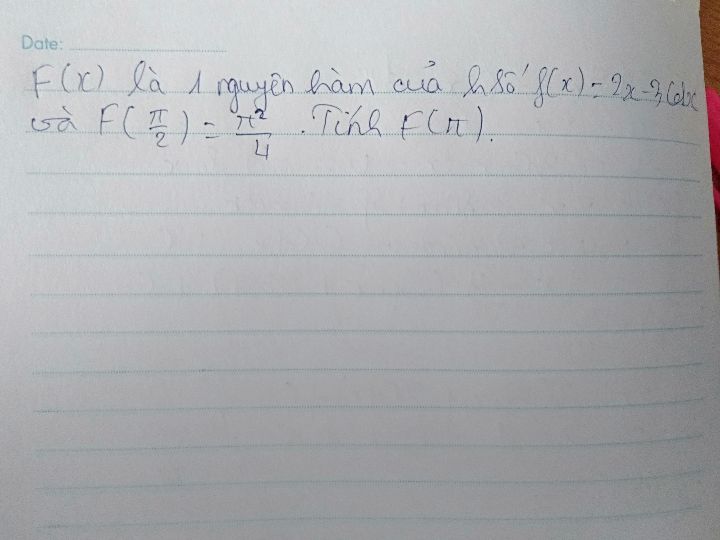 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Nguyên hàm của 4sin^2 xdx?
bởi Đinh Thị Thu Nga
 11/02/2020
11/02/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm nguyên hàm của x^2.căn(x^2-1)dx
bởi Quỳnh Như
 11/02/2020
11/02/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính giá trị F^2(e) biết F(x) là một nguyên hàm của hàm số f(x)=căn(ln^2 x+1).lnx/x
bởi Huy Đức
 11/02/2020
Giúp em ạ em cảm ơn
11/02/2020
Giúp em ạ em cảm ơn Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm nguyên hàm ln(cosx)dx
bởi tdtn
 10/02/2020
Ln(cosx)dxTheo dõi (0) 1 Trả lời
10/02/2020
Ln(cosx)dxTheo dõi (0) 1 Trả lời -


Tìm nguyên hàm của hàm số y=ln(x+2)/x^2
bởi Lê Nhựt Hào
 10/02/2020
10/02/2020
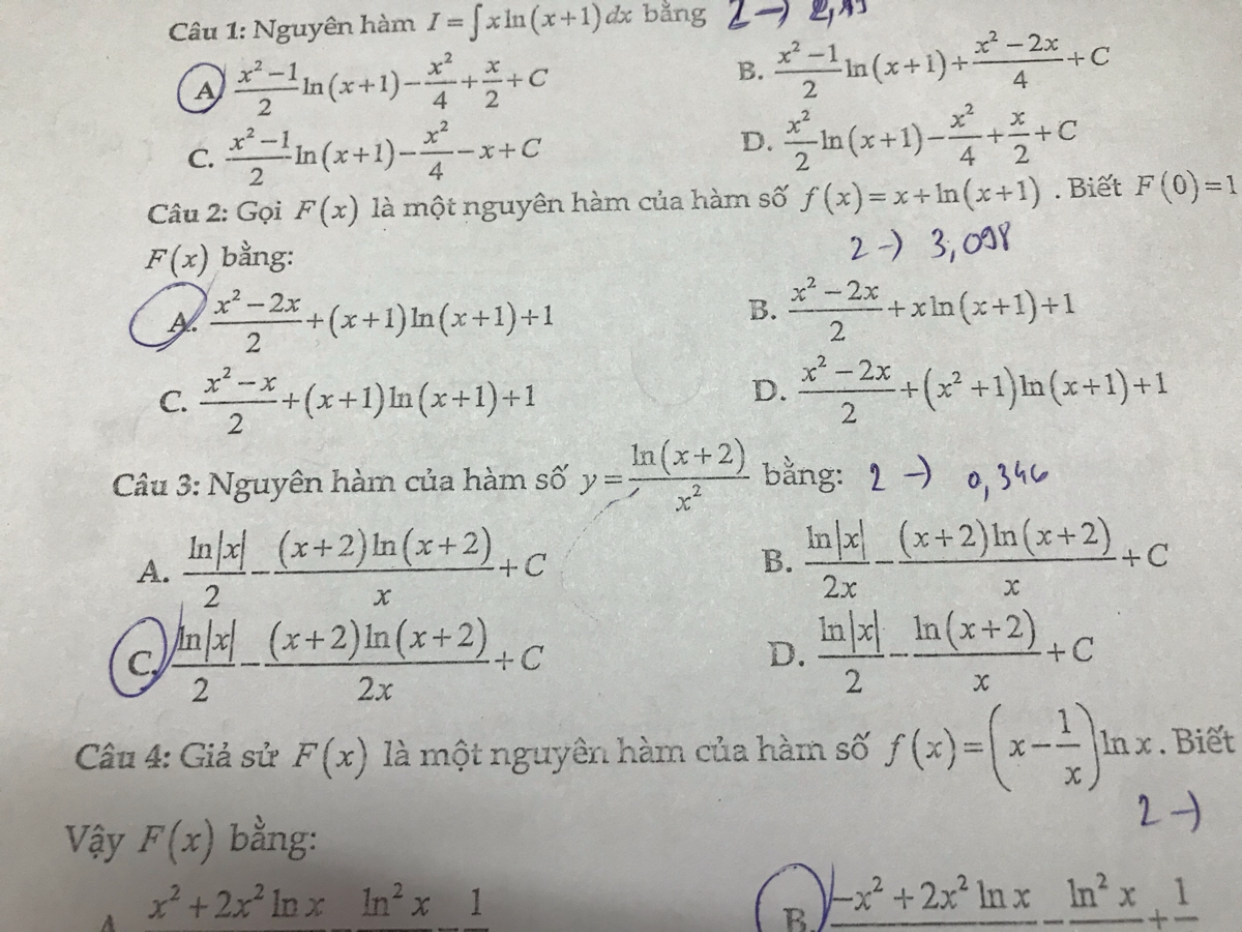 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm nguyên hàm của hàm số (1+lnx)/x^2
bởi Trần Huệ
 10/02/2020
10/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 3.9 trang 165 SBT Toán 12
Bài tập 3.10 trang 165 SBT Toán 12
Bài tập 3.12 trang 165 SBT Toán 12
Bài tập 3.13 trang 165 SBT Toán 12
Bài tập 3.14 trang 166 SBT Toán 12
Bài tập 3.15 trang 166 SBT Toán 12
Bài tập 1 trang 141 SGK Toán 12 NC
Bài tập 2 trang 141 SGK Toán 12 NC
Bài tập 3 trang 141 SGK Toán 12 NC
Bài tập 4 trang 141 SGK Toán 12 NC
Bài tập 5 trang 145 SGK Toán 12 NC
Bài tập 6 trang 145 SGK Toán 12 NC
Bài tập 7 trang 145 SGK Toán 12 NC





