Giải bài tập Toán 11 Chân trời sáng tạo Bài 3: Các công thức lượng giác

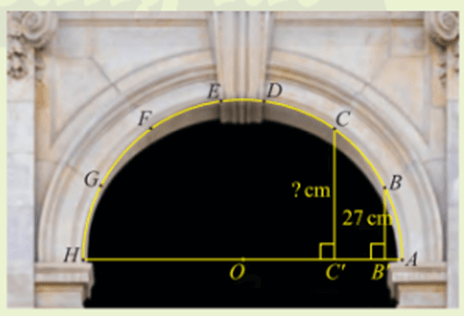
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

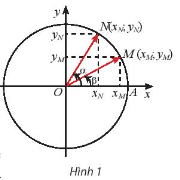
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ $\overrightarrow{OM}$ và $\overrightarrow{ON}$ sau đây:

$\overrightarrow{OM}.\overrightarrow{ON}$$= \left | \overrightarrow{OM} \right |.\left | \overrightarrow{ON} \right |cos\left ( \overrightarrow{OM}.\overrightarrow{ON} \right )$$= cos\left ( \overrightarrow{OM}.\overrightarrow{ON} \right )$$= cos(\alpha -\beta )$

$\overrightarrow{OM}.\overrightarrow{ON}$$= x_{M}.x_{N}+y_{M}.y_{N}$

Hãy suy ra công thức tính $cos(\alpha -\beta )$ theo các giá trị lượng giác của $\alpha$ và $\beta$. Từ đó, hãy suy ra công thức $cos(\alpha +\beta )$ bằng cách thay $\beta$ bằng -$\beta$.

Tính $sin(\frac{\pi }{12})$ và $tan(\frac{\pi }{12})$

Hãy áp dụng công thức cộng cho trường hợp $\beta  = \alpha$ và tính các giá trị lượng giác của góc $2\alpha$.

Tính $cos\frac{\pi }{8}$ và $tan\frac{\pi }{8}$

Từ công thức cộng, hãy tính tổng và hiệu của:

a) $cos(\alpha -\beta )$ và $cos(\alpha +\beta )$

b) $sin(\alpha -\beta )$ và $sin(\alpha +\beta )$

Tính giá trị của biểu thức $sin\frac{\pi }{24}cos\frac{5\pi }{24}$ và $sin\frac{7\pi }{8}cos\frac{5\pi }{8}$

Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác $a = \frac{\alpha +\beta }{2}$ và $b = \frac{\alpha -\beta }{2}$, ta được các đẳng thức nào?

Tính $cos\frac{7\pi }{12} + cos\frac{\pi }{12}$.

Trong bài toán khởi động, cho biết vòm cổng rộng 120cm và khoảng cách từ B đến đường kính AH là 27cm. Tính $sin\alpha$ và $cos\alpha$, từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.

Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc:

a) $\frac{5\pi }{12}$

b) $-555^{o}$

Tính $sin(\alpha +\frac{\pi }{6})$, $cos(\frac{\pi }{4}-\alpha )$ biết $sin\alpha = -\frac{5}{13}$ và $\pi <\alpha <\frac{3\pi }{2}$.

Tính các giá trị lượng giác của góc $2\alpha$, biết:

a) $sin\alpha  = \frac{\sqrt{3}}{3}$ và $0<\alpha <\frac{\pi }{2}$

b) $sin\frac{\alpha}{2}  = \frac{3}{4}$ và $\pi <\alpha <2\pi$

Rút gọn các biểu thức sau:

a) $\sqrt{2}sin(\alpha +\frac{\pi }{4}) - cos\alpha$

b) $(cos\alpha  + sin\alpha )^{2}-sin2\alpha$

Tính các giá trị lượng giác của góc $\alpha$, biết:

a) $cos2\alpha = \frac{2}{5}$ và $-\frac{\pi }{2} <\alpha < 0$

b) $sin2\alpha = -\frac{4}{9}$ và $\frac{\pi }{2} < \alpha < \frac{3\pi }{4}$

Chứng minh rằng trong tam giác ABC, ta có sinA = sinBcosC + sinC.cosB.

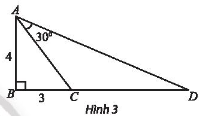
Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4, BC = 3. Vẽ điểm D nằm trên tia đối của tia CB thoả mãn $\widehat{CAD} = 30^{o}$. Tính tan$\widehat{BAD}$, từ đó tính độ dài cạnh CD.

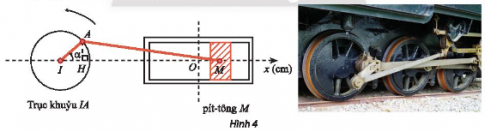
Trong Hình 4, pít-tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi-lanh làm quay trục khuỷu IA. Ban đầu I,A,M thẳng hàng. Cho $\alpha$ là góc quay của trục khuỷu, O là vị trị của pít-tông khi $\alpha =\frac{\pi }{2}$ và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8 cm, viết công thức tính toạ độ $x_{M}$ của điểm M trên trục Ox theo $\alpha$.

b) Làm tròn $\alpha =0$. Sau 1 phút chuyển động, $x_{M}$ = -3cm. Xác định $x_{M}$ sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.

Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt tua-bin gió. Biết các cánh quạt dài 31m, độ cao của điểm M so với mặt đất là 30m, góc giữa các cánh quạt là $\frac{2\pi }{3}$ và số đo góc (OA, OM) là $\alpha$

a) Tính $sin\alpha$ và $cos\alpha$

b) Tính sin của các góc lượng giác (OA, ON) và (OA, OP), từ đó tính chiều cao của các điểm N và P so với mặt đất (theo đơn vị mét). Làm tròn kết quả đến hàng phần trăm.

Không dùng máy tính cầm tay. Tính giá trị của các biểu thức sau:

a) $\sin \frac{19\pi }{24}\cos \frac{37\pi }{24};$

b) $\cos \frac{41\pi }{12}-\cos \frac{13\pi }{12};$

c) $\frac{\tan \frac{\pi }{7}+\tan \frac{3\pi }{28}}{1+\tan \frac{6\pi }{7}\tan \frac{3\pi }{28}}.$

Cho $\cos \alpha =\frac{11}{61}$ và $-\frac{\pi }{2}<\alpha <\mathrm{0,}$ tính giá trị của các biểu thức sau:

a) $\sin \left(\frac{\pi }{6}-\alpha \right);$

b) $\cot \left(\alpha +\frac{\pi }{4}\right);$

c) $\cos \left(2\alpha +\frac{\pi }{3}\right);$

d) $\tan \left(\frac{3\pi }{4}-2\alpha \right).$

Rút gọn các biểu thức sau:

a) sinxcos⁵x ‒ cosxsin⁵x;

b) $\frac{\sin 3x\cos 2x+\sin x\cos 6x}{\sin 4x};$

c) $\frac{\cos x-\cos 2x+\cos 3x}{\mathrm{s}\text{inx}-\sin 2x+\sin 3x};$

d) $\frac{2\sin \left(x+y\right)}{\cos \left(x+y\right)+\cos \left(x-y\right)}-\tan y.$

Chứng minh các đẳng thức lượng giác sau:

a) $4\cos x\cos \left(\frac{\pi }{3}-x\right)\cos \left(\frac{\pi }{3}+x\right)=\cos 3x;$

b) $\frac{\sin 2x\cos x}{\left(1+\cos x\right)\left(1+\cos 2x\right)}=\tan \frac{x}{2};$

c) sinx(1 + 2cos2x + 2cos4x + 2cos6x) = sin7x;

d) $\frac{{\sin }^{2}3x}{{\sin }^{2}x}-\frac{{\cos }^{2}3x}{{\text{cos}}^{2}x}=8\cos 2x.$

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

a) ${\sin }^{2}x+\cos \left(\frac{\pi }{3}-x\right)\cos \left(\frac{\pi }{3}+x\right);$

b) $\cos \left(x-\frac{\pi }{3}\right)\cos \left(x+\frac{\pi }{4}\right)+\cos \left(x+\frac{\pi }{6}\right)\cos \left(x+\frac{3\pi }{4}\right).$

Cho tam giác ABC, chứng minh rằng:

a) cosAcosB ‒ sinAsinB + cosC = 0;

b) $\cos \frac{B}{2}\sin \frac{C}{2}+\sin \frac{B}{2}\cos \frac{C}{2}=\cos \frac{A}{2}.$

Cho sinα + cosα = m. Tìm m để $\sin 2\alpha =-\frac{3}{4}?$

Cho $\sin \alpha =\frac{3}{5},$ $\cos \beta =\frac{12}{13}$ và 0° < α, β < 90°. Tính giá trị của biểu thức sin(α + β) và cos(α ‒ β)?

Không sử dụng máy tính cầm tay, tính giá trị của các biểu thức sau:

a) sin6°cos12°cos24°cos48°;

b) cos68°cos78° + cos22°cos12° + cos190°.

Phương trình dao động điều hòa của một vật tại thời điểm t giây được cho bởi công thức x(t) = Acos(ωt + φ), trong đó x(t) (cm) là li độ của một vật tại thời điểm t giây, A là biên độ dao động (A > 0) và φ ∈ [‒π; π] là pha ban đầu của dao động.

Xét hai dao động điều hòa có phương trình lần lượt là:

$x_1\left(t\right)=3\cos \left(\frac{\pi }{4}t+\frac{\pi }{3}\right)$ (cm) và $x_2\left(t\right)=3\cos \left(\frac{\pi }{4}t-\frac{\pi }{6}\right)$(cm).

a) Xác định phương trình dao động tổng hợp x(t) = x₁(t) + x₂(t).

b) Tìm biên độ và pha ban đầu của dao động tổng hợp trên.