Hoạt động khám phá 1 trang 21 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

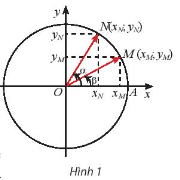
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow{OM}\) và \(\overrightarrow{ON}\) sau đây:

\(\overrightarrow{OM}.\overrightarrow{ON} \)\(= \left | \overrightarrow{OM} \right |.\left | \overrightarrow{ON} \right |cos\left ( \overrightarrow{OM}.\overrightarrow{ON} \right ) \)\(= cos\left ( \overrightarrow{OM}.\overrightarrow{ON} \right ) \)\(= cos(\alpha -\beta )\)

\(\overrightarrow{OM}.\overrightarrow{ON} \)\(= x_{M}.x_{N}+y_{M}.y_{N}\)

Hãy suy ra công thức tính \(cos(\alpha -\beta )\) theo các giá trị lượng giác của \(\alpha \) và \(\beta \). Từ đó, hãy suy ra công thức \(cos(\alpha +\beta )\) bằng cách thay \(\beta \) bằng -\(\beta \).