Hoạt động khởi động trang 20 SGK Toán 11 Chân trời sáng tạo tập 1
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?
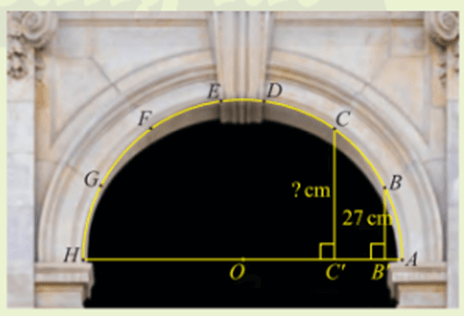
Hướng dẫn giải chi tiết Hoạt động khởi động
Phương pháp giải
Dùng công thức nhân đôi sau: sin2a = 2sinacosa
Lời giải chi tiết
Đặt chiều rộng cổng AH = d.
⇒ OA = OB = d.
Xét tam giác OBB’ vuông tại B’, có:
.
Vì \( \overset\frown{AC}= \overset\frown{BC}\) nên sđ\( \overset\frown{AC}\) = 2.sđ\(\overset\frown{AB}\)
Xét tam giác OCC’ vuông tại C’, có:
\(\sin \widehat {COC'} = \frac{{CC'}}{{OC}} \)\(\Leftrightarrow CC' = OC\sin \widehat {COC'} = OC\sin \left( {2\widehat {BOB'}} \right)\)
Sau bài học này ta sẽ giải quyết tiếp được bài toán như sau:
\(\sin \left( {2\widehat {BOB'}} \right) \)\(= 2\sin \widehat {BOB'}\cos \widehat {BOB'} \)\(= 2.\frac{{54}}{d}.\sqrt {1 - {{\left( {\frac{{54}}{d}} \right)}^2}} \)\(= \frac{{108}}{d}\sqrt {1 - {{\left( {\frac{{54}}{d}} \right)}^2}} \)
Vậy khoảng cách này từ điểm C đến AH là .
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Hoạt động khám phá 1 trang 21 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 21 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 21 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 22 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 22 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 22 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 22 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 23 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 23 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 23 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 23 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 7 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 8 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 9 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 19 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 19 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 19 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 19 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 6 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 7 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 8 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 9 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 10 trang 20 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST





