Giải Bài 8 trang 24 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST

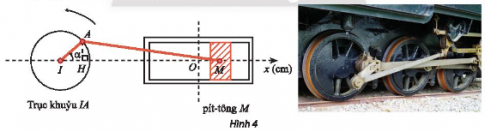
Trong Hình 4, pít-tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi-lanh làm quay trục khuỷu IA. Ban đầu I,A,M thẳng hàng. Cho \(\alpha \) là góc quay của trục khuỷu, O là vị trị của pít-tông khi \(\alpha =\frac{\pi }{2}\) và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8 cm, viết công thức tính toạ độ \(x_{M}\) của điểm M trên trục Ox theo \(\alpha \).

b) Làm tròn \(\alpha =0\). Sau 1 phút chuyển động, \(x_{M}\) = -3cm. Xác định \(x_{M}\) sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.