Phần hướng dẫn giải bài tập SGK bài 1 Vectơ trong không gian sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập liên quan đến vectơ trong không gian như chứng minh các đẳng thức vectơ, vectơ đồng phẳng,...từ SGK Hình học 11 Cơ bản và Nâng cao.
-
Bài tập 1 trang 91 SGK Hình học 11
Cho hình lăng trụ tứ giác: ABCD.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB', CC', DD' lần lượt tại I, K, L, M. xét các véctơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. hãy chỉ ra các véctơ:
a) Các véctơ cùng phương với \(\overrightarrow{IA}\);
b) Các véctơ cùng hướng với \(\overrightarrow{IA}\);
c) Các véctơ ngược hướng với \(\overrightarrow{IA}\).
-
Bài tập 2 trang 91 SGK Hình học 11
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
a) \(\overrightarrow{AB} + \overrightarrow{B'C'} + \overrightarrow{DD'} = \overrightarrow{AC'};\)
b) \(\overrightarrow{BD} - \overrightarrow{D'D} - \overrightarrow{B'D'} = \overrightarrow{BB'};\)
c) \(\overrightarrow{AC} + \overrightarrow{BA'} + \overrightarrow{DB} + \overrightarrow{C'D} = \overrightarrow{0}.\)
-
Bài tập 3 trang 91 SGK Hình học 11
Cho hình bình hành ABCD. Gọi S là một điểm nằm ngoài mặt phẳng chứa hình bình hành. Chứng minh rằng: \(\overrightarrow{SA}\) + \(\overrightarrow{SC}\) = \(\overrightarrow{SB}\) + \(\overrightarrow{SD}\).
-
Bài tập 4 trang 91 SGK Hình học 11
Cho hình tứ diện ABCD. Gọi M và N lần lượt là trủng điểm của AB và CD. Chứng minh rằng:
a) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AD}+\overrightarrow{BC} \right );\)
b) \(\overrightarrow{MN}=\frac{1}{2}\left ( \overrightarrow{AC}+\overrightarrow{BD} \right).\)
-
Bài tập 5 trang 92 SGK Hình học 11
Cho hình tứ diện ABCD. Hãy xác định hai điểm E, F sao cho:
a) \(\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD};\)
b) \(\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{AD}.\)
-
Bài tập 6 trang 92 SGK Hình học 11
Cho hình tứ diện ABCD. Gọi G là trọng tâm tam giác ABC. Chứng minh rằng: \(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}.\)
-
Bài tập 7 trang 92 SGK Hình học 11
Gọi M và N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm của đoạn thẳng MN và P là một điểm bất kì trong không gian. Chứng minh rằng:
a) \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\)
b) \(\overrightarrow{PI}=\frac{1}{4}(\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD})\)
-
Bài tập 8 trang 92 SGK Hình học 11
Cho hình lăng trụ tam giác ABC.A'B'C' có \(\overrightarrow{AA}\) = \(\overrightarrow{a}\), \(\overrightarrow{AB}\) = \(\overrightarrow{b}\), \(\overrightarrow{AC}\) = \(\overrightarrow{c}\). Hãy phân tích (hay biểu thị véctơ \(\overrightarrow{B'C}\), \(\overrightarrow{BC'}\) qua các véctơ \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{c}\).
-
Bài tập 9 trang 92 SGK Hình học 11
Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho \(\overrightarrow{MS}\) = \(-2\overrightarrow{MA}\) và trên đoạn BC lấy điểm N sao cho \(\overrightarrow{NB}=-\frac{1}{2}\overrightarrow{NC}.\) Chứng minh rằng ba véctơ \(\overrightarrow{AB}\), \(\overrightarrow{MN}\), \(\overrightarrow{SC}\) đồng phẳng.
-
Bài tập 10 trang 92 SGK Hình học 11
Cho hình hộp ABCD.EFGH. Gọi K là giao điểm của AH và DE, I là giao điểm của BH và DF. Chứng minh ba véctơ \(\overrightarrow{AC}, \overrightarrow{KI}, \overrightarrow{FG}\) đồng phẳng.
-
Bài tập 3.1 trang 129 SBT Hình học 11
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ \(\overrightarrow {AO} ,\overrightarrow {AO'} \), theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \(\overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB} \)
-
Bài tập 3.2 trang 129 SBT Hình học 11
Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
-
Bài tập 3.3 trang 129 SBT Hình học 11
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
\(\frac{{AM}}{{AC}} = \frac{{BN}}{{BD}} = k\left( {k > 0} \right)\)
Chứng minh rằng ba vectơ \(\overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
-
Bài tập 3.4 trang 130 SBT Hình học 11
Cho hình lăng trụ tam giác ABC.A'B'C' có độ dài cạnh bên bằng a. Trên các cạnh bên AA', BB', CC' ta lấy tương ứng các điểm M, N, P sao cho AM + BN + CP = a
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.
-
Bài tập 3.5 trang 130 SBT Hình học 11
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) đồng phẳng.
-
Bài tập 3.6 trang 130 SBT Hình học 11
Trên mặt phẳng (α) cho hình bình hành A1B1C1D1. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A2B2C2D2. Trên các đoạn A1A2, B1B2, C1C2, D1D2 ta lần lượt lấy các điểm A, B, C, D sao cho
\(\frac{{A{A_1}}}{{A{A_2}}} = \frac{{B{B_1}}}{{B{B_2}}} = \frac{{C{C_1}}}{{C{C_2}}} = \frac{{D{D_1}}}{{D{D_2}}} = 3\)
Chứng minh rằng tứ giác ABCD là hình bình hành.
-
Bài tập 3.7 trang 130 SBT Hình học 11
Cho hình hộp ABCD.A'B'C'D' có P và R lần lượt là trung điểm các cạnh AB và A'D'. Gọi P', Q, Q' lần lượt là tâm đối xứng của các hình bình hành ABCD, CDD'C', A'B'C'D', ADD'A'
a) Chứng minh rằng \(\overrightarrow {PP'} + \overrightarrow {QQ'} + \overrightarrow {RR'} = \overrightarrow 0 \)
b) Chứng minh hai tam giác PQR và P'Q'R' có trọng tâm trùng nhau.
-
Bài tập 1 trang 91 SGK Hình học 11 NC
Ba vecto \(\vec a,\vec b,\vec c\) có đồng phẳng không nếu một trong hai điều sau đây xảy ra ?
a. Có một vecto trong ba vecto đó bằng \(\overrightarrow 0 \)
b. Có hai vecto trong ba vecto đó cùng phương.
-
Bài tập 2 trang 91 SGK Toán 11 NC
Cho hình chóp S.ABCD
a. Chứng minh rằng nếu ABCD là hình bình hành thì \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \). Điều ngược lại có đúng không ?
b. Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 4\overrightarrow {SO} \)
-
Bài tập 3 trang 91 SGK Hình học 11 NC
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của hai đường thẳng AB’ và A’B. Chứng minh rằng các đường thẳng GI và CG’ song song với nhau.
-
Bài tập 4 trang 91 SGK Hình học 11 NC
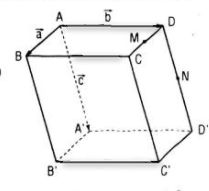
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
-
Bài tập 5 trang 91 SGK Hình học 11 NC
Trong không gian cho tam giác ABC.
a. Chứng minh rằng nếu điểm M thuộc mp(ABC) thì có ba số x, y, z mà x + y + z = 1 sao cho \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \) với mọi điểm O.
b. Ngược lại, nếu có một điểm O trong không gian sao cho \(\overrightarrow {OM} = x\overrightarrow {OA} + y\overrightarrow {OB} + z\overrightarrow {OC} \), trong đó x + y + z = 1 thì điểm M thuộc mp(ABC).
-
Bài tập 6 trang 91 SGK Hình học 11 NC
Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.






