Giải bài 2 tr 91 sách GK Toán Hình lớp 11
Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng:
a) \(\overrightarrow{AB} + \overrightarrow{B'C'} + \overrightarrow{DD'} = \overrightarrow{AC'};\)
b) \(\overrightarrow{BD} - \overrightarrow{D'D} - \overrightarrow{B'D'} = \overrightarrow{BB'};\)
c) \(\overrightarrow{AC} + \overrightarrow{BA'} + \overrightarrow{DB} + \overrightarrow{C'D} = \overrightarrow{0}.\)
Hướng dẫn giải chi tiết
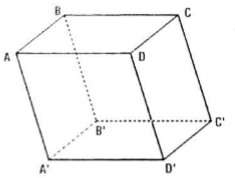
Câu a:
\(\overrightarrow{AB} + \overrightarrow{B'C'} + \overrightarrow{DD'} = \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'};\)
Câu b:
\(\overrightarrow{BD} - \overrightarrow{D'D} - \overrightarrow{B'D'} = \overrightarrow{BD} + \overrightarrow{DD'} + \overrightarrow{D'B'} = \overrightarrow{BB'};\)
Câu c:
\(\overrightarrow{AC} + \overrightarrow{BA'} + \overrightarrow{DB} + \overrightarrow{C'D}\)
\(=(\overrightarrow{AB}+\overrightarrow{AD})+ (\overrightarrow{BA}+\overrightarrow{BB})+ (\overrightarrow{DA}+\overrightarrow{DC})+ (\overrightarrow{C'C}+\overrightarrow{C'D})\)
\(=(\overrightarrow{AB}+\overrightarrow{BA})+ (\overrightarrow{AD}+\overrightarrow{DA})+ (\overrightarrow{BB'}+\overrightarrow{C'C})+ (\overrightarrow{DC}+\overrightarrow{C'D})\)
\(=\overrightarrow{0}\)
-- Mod Toán 11 HỌC247
Video hướng dẫn giải SGK
Để luyện tập thêm dạng bài tương tự như Bài tập 2 trang 91 trong SGK các em làm thêm câu hỏi trắc nghiệm sau để cũng cố kỹ năng làm dạng bài.
-
Câu 1:
Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là:
- A. Mặt phẳng trung trực của đoạn thẳng AB.
- B. Đường trung trực của đoạn thẳng AB .
- C. Mặt phẳng vuông góc với AB tại A .
- D. Đường thẳng qua A và vuông góc với AB .
-
Bài 3.6 trang 132 sách bài tập Hình học 11
bởi thi trang
24/10/2018
Bài 3.6 (Sách bài tập - trang 132)Trên mặt phẳng \(\left(\alpha\right)\) cho hình bình hành \(A_1B_1C_1D_1\). Về một phía đối với mặt phẳng \(\left(\alpha\right)\) ta dựng hình bình hành \(A_2B_2C_2D_2\). Trên các đoạn \(A_1A_2,B_1B_2,C_1C_2,D_1D_2\) ta lần lượt lấy các điểm A, B, C, D sao cho :
\(\dfrac{AA_1}{AA_2}=\dfrac{BB_1}{BB_2}=\dfrac{CC_1}{CC_2}=\dfrac{DD_1}{DD_2}=3\)
Chứng minh rằng tứ giác ABCD là hình bình hành ?
Theo dõi (0) 1 Trả lời
Được đề xuất cho bạn
