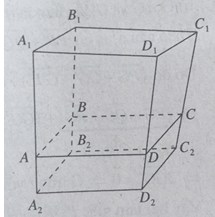
Lấy điểm O cố định rồi đặt \(\overrightarrow {O{A_1}} = \overrightarrow {{a_1}} ,\overrightarrow {O{B_1}} = \overrightarrow {{b_1}} ,\overrightarrow {O{C_1}} = \overrightarrow {{c_1}} ,\overrightarrow {O{D_1}} = \overrightarrow {{d_1}} \)
Điều kiện cần và đủ để tứ giác A1B1C1D1 là hình bình hành là:
\(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) (theo bài 3.2) (1)
Đặt \(\overrightarrow {O{A_2}} = \overrightarrow {{a_2}} ,\overrightarrow {O{B_2}} = \overrightarrow {{b_2}} ,\overrightarrow {O{C_2}} = \overrightarrow {{c_2}} ,\overrightarrow {O{D_2}} = \overrightarrow {{d_2}} \)
Điều kiện cần và đủ để tứ giác A2B2C2D2 là hình bình hành là:
\(\overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}} \,\,\,\left( 2 \right)\)
Đặt \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c ,\overrightarrow {OD} = \overrightarrow d \)
Ta có \(\frac{{A{A_1}}}{{A{A_2}}} = 3 \Rightarrow \overrightarrow {A{A_1}} = - 3\overrightarrow {A{A_2}} \)
\(\begin{array}{l}
\Leftrightarrow \overrightarrow {O{A_1}} - \overrightarrow {OA} = - 3\left( {\overrightarrow {O{A_2}} - \overrightarrow {OA} } \right)\\
\Leftrightarrow \overrightarrow {{a_1}} - \overrightarrow a = - 3\left( {\overrightarrow {{a_2}} - \overrightarrow a } \right)\\
\Leftrightarrow \overrightarrow a = \frac{1}{4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right)
\end{array}\)
Tương tự: \(\overrightarrow b = \frac{1}{4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right),\overrightarrow c = \frac{1}{4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right),\overrightarrow d = \frac{1}{4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{d_2}} } \right)\)
Ta có: \(\overrightarrow a + \overrightarrow c = \frac{1}{4}\left( {\overrightarrow {{a_1}} + 3\overrightarrow {{a_2}} } \right) + \frac{1}{4}\left( {\overrightarrow {{c_1}} + 3\overrightarrow {{c_2}} } \right) = \frac{1}{4}\left( {\overrightarrow {{a_1}} + \overrightarrow {{c_1}} } \right) + \frac{3}{4}\left( {\overrightarrow {{a_2}} + \overrightarrow {{c_2}} } \right)\)
Và \(\overrightarrow b + \overrightarrow d = \frac{1}{4}\left( {\overrightarrow {{b_1}} + 3\overrightarrow {{b_2}} } \right) + \frac{1}{4}\left( {\overrightarrow {{d_1}} + 3\overrightarrow {{d_2}} } \right) = \frac{1}{4}\left( {\overrightarrow {{b_1}} + \overrightarrow {{d_1}} } \right) + \frac{3}{4}\left( {\overrightarrow {{b_2}} + \overrightarrow {{d_2}} } \right)\)
Từ (1) và (2) ta có \(\overrightarrow {{a_1}} + \overrightarrow {{c_1}} = \overrightarrow {{b_1}} + \overrightarrow {{d_1}} \) và \(\overrightarrow {{a_2}} + \overrightarrow {{c_2}} = \overrightarrow {{b_2}} + \overrightarrow {{d_2}}\) nên suy ra \(\overrightarrow a + \overrightarrow c = \overrightarrow b + \overrightarrow d \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \) \( \Leftrightarrow \) tứ giác ABCD là hình bình hành.
-- Mod Toán 11 HỌC247






