Bài tập 4 trang 91 SGK Hình học 11 NC
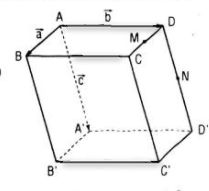
Cho hình hộp ABCD.A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Hướng dẫn giải chi tiết
Đặt \(\overrightarrow {AB} = \overrightarrow a ;\overrightarrow {AD} = \overrightarrow b ;\overrightarrow {AA'} = \overrightarrow c \)
Vì G là trọng tâm tứ diện BCC'D nên ta có:
\(\overrightarrow {AG'} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AC'} + \overrightarrow {AD'} } \right)\)
Và G là trọng tâm tứ diện A’D’MN nên
\(\begin{array}{l}
\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AA'} + \overrightarrow {AD'} + \overrightarrow {AM} + \overrightarrow {AN} } \right)\\
\Rightarrow \overrightarrow {GG'} = \overrightarrow {AG'} - \overrightarrow {AC} \\
= \frac{1}{4}\left( {\overrightarrow {A'B} + \overrightarrow {D'C} + \overrightarrow {MC'} + \overrightarrow {ND'} } \right)\\
= \frac{1}{4}\left( {\overrightarrow a - \overrightarrow c + \overrightarrow a - \overrightarrow c + \frac{1}{2}\overrightarrow a + \overrightarrow c + \frac{1}{2}\overrightarrow c } \right)\\
= \frac{1}{8}\left( {5\overrightarrow a - \overrightarrow c } \right) = \frac{1}{8}\left( {5\overrightarrow {AB} - \overrightarrow {AA'} } \right)
\end{array}\)
Do đó \(\overrightarrow {AB} ,\overrightarrow {AA'} ,\overrightarrow {GG'} \) đồng phẳng.
Mặt khác, G không thuộc mặt phẳng (ABB’A’) nên đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
-- Mod Toán 11 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





