Giải bài 3.5 tr 130 SBT Hình học 11
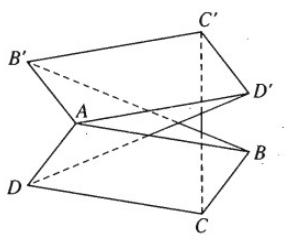
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \) đồng phẳng.
Hướng dẫn giải chi tiết
Ta có: \(\overrightarrow {BB'} = \overrightarrow {BA} + \overrightarrow {AB'} ,\overrightarrow {DD'} = \overrightarrow {DA} + \overrightarrow {AD'} \)
Do đó: \(\overrightarrow {BB'} = \overrightarrow {BA} + \overrightarrow {AB'} ,\overrightarrow {DD'} = \overrightarrow {DA} + \overrightarrow {AD'} \)
Vì \(\overrightarrow {BA} = \overrightarrow {CD} ,\overrightarrow {AB'} + \overrightarrow {AD'} = \overrightarrow {AC'} \) nên \(\overrightarrow {BB'} + \overrightarrow {DD'} = \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right) + \overrightarrow {AC'} \)
Vậy \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CA} + \overrightarrow {AC'} = \overrightarrow {CC'} \)
Hệ thức \(\overrightarrow {BB'} + \overrightarrow {DD'} = \overrightarrow {CC'} \) biểu thị sự đồng phẳng của ba vectơ \(\overrightarrow {BB'} ,\overrightarrow {CC'} ,\overrightarrow {DD'} \)
-- Mod Toán 11 HỌC247
-


Tính góc giữu mp (MBD) và mp(ABCD) biết S.ABCD là hình chóp tứ giác đều
bởi Trần Thị Trang
 24/10/2018
24/10/2018
Cho hình chóp tứ giác đều S.ABCD, cạnh đáy bằng a, cạnh bên bằng \(\frac{a\sqrt{5}}{2}\).Gọi O là tâm hình vuông ABCD và M là trung điểm SC.
a) CM (MBD) vuông góc với (SAC)
b)Góc (SA,(ABCD))=?
c)Góc ((MBD),(ABCD))=?
d)Góc ((SAB),(ABCD))=?
mọi người giúp em câu b với c nhé, cảm ơn mọi người nhiều
Theo dõi (0) 1 Trả lời -


giúp em với
bởi Mai Hoa
 01/08/2018
01/08/2018
Cho tứ diện đều ABCD, M là trung điểm của cạnh BC . Khi đó cos(AB,DM) bằng:
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 3.3 trang 129 SBT Hình học 11
Bài tập 3.4 trang 130 SBT Hình học 11
Bài tập 3.6 trang 130 SBT Hình học 11
Bài tập 3.7 trang 130 SBT Hình học 11
Bài tập 1 trang 91 SGK Hình học 11 NC
Bài tập 2 trang 91 SGK Toán 11 NC
Bài tập 3 trang 91 SGK Hình học 11 NC
Bài tập 4 trang 91 SGK Hình học 11 NC