Bài tập 3.1 trang 129 SBT Hình học 11

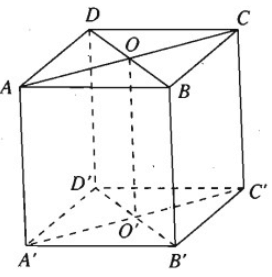
a) Ta có:

\({\overrightarrow {AO}  = \frac{1}{2}\overrightarrow {AC}  = \frac{1}{2}\overrightarrow {A'C'}  = \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) = \overrightarrow {AB}  + \overrightarrow {BO}  = \overrightarrow {AB}  + \frac{1}{2}\overrightarrow {BD} ,...}\)

\(\begin{array}{l}
\overrightarrow {AO'}  = \frac{1}{2}\overrightarrow {AC}  + \overrightarrow {AA'}  = \frac{1}{2}\left( {\overrightarrow {AA'}  + \overrightarrow {AC'} } \right) = \frac{1}{2}\left( {\overrightarrow {AB'}  + \overrightarrow {AD'} } \right)\\
 = \overrightarrow {AA'}  + \overrightarrow {A'B'}  + \frac{1}{2}\overrightarrow {B'D'}  = \overrightarrow {AB}  + \overrightarrow {BB'}  + \frac{1}{2}\overrightarrow {B'D'} ,...
\end{array}\)

b) Ta có \(\overrightarrow {AD}  + \overrightarrow {D'C'}  + \overrightarrow {D'A'}  = \overrightarrow {AD}  + \overrightarrow {DC}  + \overrightarrow {CB} \)

Vì \(\overrightarrow {D'C'}  = \overrightarrow {DC} \) và \(\overrightarrow {CB} \) nên \(\overrightarrow {AD}  + \overrightarrow {D'C'}  + \overrightarrow {D'A'}  = \overrightarrow {AB} \)

-- Mod Toán 11 HỌC247