Giải bài 1.30 tr 38 SBT Toán 11
Giải các phương trình sau
a) 1+sinx−cosx−sin2x + 2cos2x = 0
b) \(\sin x - \frac{1}{{\sin x}} = {\sin ^2}x - \frac{1}{{{{\sin }^2}x}}\)
c) cosxtan3x = sin5x
d) 2tan2x+3tanx2cot2x+3cotx+2 = 0
Hướng dẫn giải chi tiết
a) 1+sinx−cosx - sin2x+2cos2x = 0
⇔ (1−sin2x)+(sinx−cosx)+2cos2x = 0
⇔ (sinx−cosx)2+(sinx−cosx) + 2(cos2x-sin2x) = 0
⇔ (sinx−cosx)[sinx−cosx+1−2(cosx+sinx)] = 0
⇔ (sinx−cosx)(1−sinx−3cosx) = 0
\(\begin{array}{l}
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\sin x - \cos x = 0}\\
{1 - \sin x - 3\cos x = 0}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\sin x = \cos x}\\
{\sin x + 3\cos x = 1}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\tan x = 1{\rm{(1)}}}\\
{\frac{1}{{\sqrt {10} }}\sin x + \frac{3}{{\sqrt {10} }}\cos x = \frac{1}{{\sqrt {10} }}{\rm{(2)}}}
\end{array}} \right.\\
{\rm{(1)}} \Leftrightarrow x = \frac{\pi }{4} + k\pi ,k \in Z
\end{array}\)
Giải phương trình (2) ta đặt \[\frac{1}{{\sqrt {10} }} = \sin \alpha \) và \[\frac{3}{{\sqrt {10} }} = \cos \alpha \) ta được \[\cos \alpha \cos x + \sin \alpha \sin x = \frac{1}{{\sqrt {10} }}\)
\(\begin{array}{l}
\Leftrightarrow \cos (x - \alpha ) = \frac{1}{{\sqrt {10} }}\\
\Leftrightarrow x - \alpha = \pm \arccos \frac{1}{{\sqrt {10} }},k \in Z\\
\Leftrightarrow x = \alpha \pm \arccos \frac{1}{{\sqrt {10} }},k \in Z
\end{array}\)
Vậy phương trình có nghiệm là: \(x = \frac{\pi }{4} + k\pi ,k \in Z\) và \(x = \alpha \pm \arccos \frac{1}{{\sqrt {10} }},k \in Z\).
b) ĐKXĐ: sinx ≠ 0
Ta có: \(\sin x - \frac{1}{{\sin x}} = {\sin ^2}x - \frac{1}{{{{\sin }^2}x}}\)
\(\begin{array}{l}
\Leftrightarrow (\sin x - {\sin ^2}x) + \left( {\frac{1}{{{{\sin }^2}x}} - \frac{1}{{\sin x}}} \right) = 0\\
\Leftrightarrow \sin x(1 - \sin x) + \frac{{1 - \sin x}}{{{{\sin }^2}x}} = 0\\
\Leftrightarrow (1 - \sin x)({\sin ^3}x + 1) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
\sin x = 1\\
\sin x = - 1
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{2} + k2\pi ,k \in Z\\
x = - \frac{\pi }{2} + k2\pi ,k \in Z
\end{array} \right.\\
\Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in Z
\end{array}\)
c) ĐKXĐ: cos3x ≠ 0
\( \Leftrightarrow x \ne \frac{\pi }{6} + k\frac{\pi }{3},k \in Z\)
Ta có: cosxtan3x = sin5x
\( \Leftrightarrow \cos x\frac{{\sin 3x}}{{\cos 3x}} = \sin 5x\)
⇔ cosxsin3x = sin5xcos3x
\( \Leftrightarrow \frac{1}{2}(\sin 4x + \sin 2x) = \frac{1}{2}(\sin 8x + \sin 2x)\)
⇔ sin8x = sin4x
\(\begin{array}{l}
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{8x = 4x + k2\pi ,k \in Z}\\
{8x = \pi - 4x + k2\pi ,k \in Z}
\end{array}} \right.\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = k\frac{\pi }{2},k \in Z}\\
{x = \frac{\pi }{{12}} + k\frac{\pi }{6},k \in Z}
\end{array}} \right.
\end{array}\)
Kết hợp với ĐKXĐ ta được nghiệm của phương trình là x = kπ, k∈Z và \(x = \frac{\pi }{{12}} + k\frac{\pi }{6},k \in Z\).
d) ĐKXĐ: cosx ≠ 0 và sinx ≠ 0.
Ta có: 2tan2x+3tanx+2cot2x+3cotx+2 = 0
⇔ (2tan2x+2cot2x)+(3tanx+3cotx)+2 = 0
⇔ 2[(tanx+cotx)2−2tanxcotx]+3(tanx+cotx)+2=0
⇔2[(tanx+cotx)2−2]+3(tanx+cotx)+2 = 0
Đặt tanx+cotx = t ta được phương trình 2t2+3t−2 = 0
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = - 2}\\
{t = \frac{1}{2}}
\end{array}} \right.\)
Với t = −2 ta có tanx+cotx = −2
⇒ tanx+1tanx = −2
⇒ tan2x+1 = −2tanx
⇒ tanx = −1
\( \Rightarrow x = - \frac{\pi }{4} + k\pi ,k \in Z\) (thỏa mãn)
Với \(t=\frac{1}{2}\) ta có \(\tan x + \cot x = \frac{1}{2}\)
\( \Rightarrow \tan x + \frac{1}{{\tan x}} = \frac{1}{2}\)
⇒ 2tan2x+2 = tanx (Vô nghiệm)
Vậy phương trình có nghiệm là \(x = - \frac{\pi }{4} + k\pi ,k \in Z\).
-- Mod Toán 11 HỌC247
-


Trong các phương trình sau, phương trình nào vô nghiệm?
bởi Lê Vinh
 24/01/2021
24/01/2021
A. sinx + 3 = 0
B. 2cos2x -cosx – 1 = 0
C. tanx + 3 = 0
D. 3sinx – 2 = 0
Theo dõi (0) 1 Trả lời -


Nghiệm của phương trình \(5\left( {1 + cosx} \right) = si{n^4}x + co{s^4}x\) là:
bởi Nguyễn Vũ Khúc
 24/01/2021
Theo dõi (0) 1 Trả lời
24/01/2021
Theo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị của tham số m để phương trình \(2si{n^2}x + msin2x = 2m\) vô nghiệm.
bởi Lê Văn Duyệt
 24/01/2021
24/01/2021
A. 0 ≤ m ≤ 4/3.
B. m < 0, m > 4/3.
C. 0 < m < 4/3.
D. m < -4/3, m > 0.
Theo dõi (0) 1 Trả lời -


Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình \(11si{n^2}\;x{\rm{ }} + {\rm{ }}\left( {m - 2} \right)sin2x + 3co{s^2}x = 2\) có nghiệm?
bởi Bin Nguyễn
 25/01/2021
25/01/2021
A. 16
B. 21
C. 15
D. 6
Theo dõi (0) 1 Trả lời -


Nghiệm dương nhỏ nhất của phương trình \(4si{n^2}\;x + 3\sqrt 3 {\rm{ }}sin2x - 2co{s^2}x = 4\) là:
bởi Nguyễn Thanh Hà
 25/01/2021
25/01/2021
A. π/12.
B. π/6.
C. π/4.
D. π/3.
Theo dõi (0) 1 Trả lời -


Số vị trí biểu diễn các nghiệm phương trình \(si{n^2}x - 4sinxcosx + 4co{s^2}x = 5\) trên đường tròn lượng giác là?
bởi Nhi Nhi
 25/01/2021
25/01/2021
A. 4.
B.3.
C.2.
D. 1.
Theo dõi (0) 1 Trả lời -


Nghiệm của phương trình \(si{n^2}x--sinxcosx = 1\) là:
bởi A La
 24/01/2021
Theo dõi (0) 1 Trả lời
24/01/2021
Theo dõi (0) 1 Trả lời -


A. m = 4
B. m ≥ 4
C. m ≤ 4
D. m ∈ R
Theo dõi (0) 1 Trả lời -


Giải phương trình 6cos2x + sinx -1 = 0
bởi Phạm Ngọc Anh Đức
 14/09/2020
14/09/2020
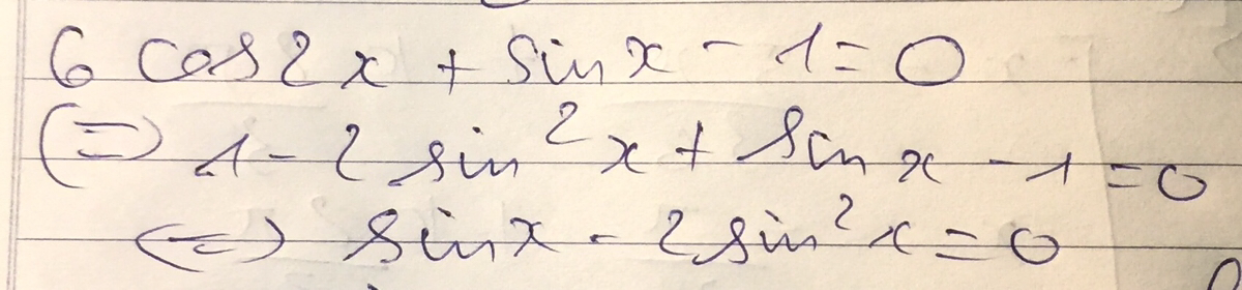 Theo dõi (2) 2 Trả lời
Theo dõi (2) 2 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình: (frac{{({{sin }^2} - 1)({{cos }^2}x + {{sin }^2}x)}}{{cos x.sin x}})
bởi Nhi Nhi
 12/09/2020
Giải pt
12/09/2020
Giải pt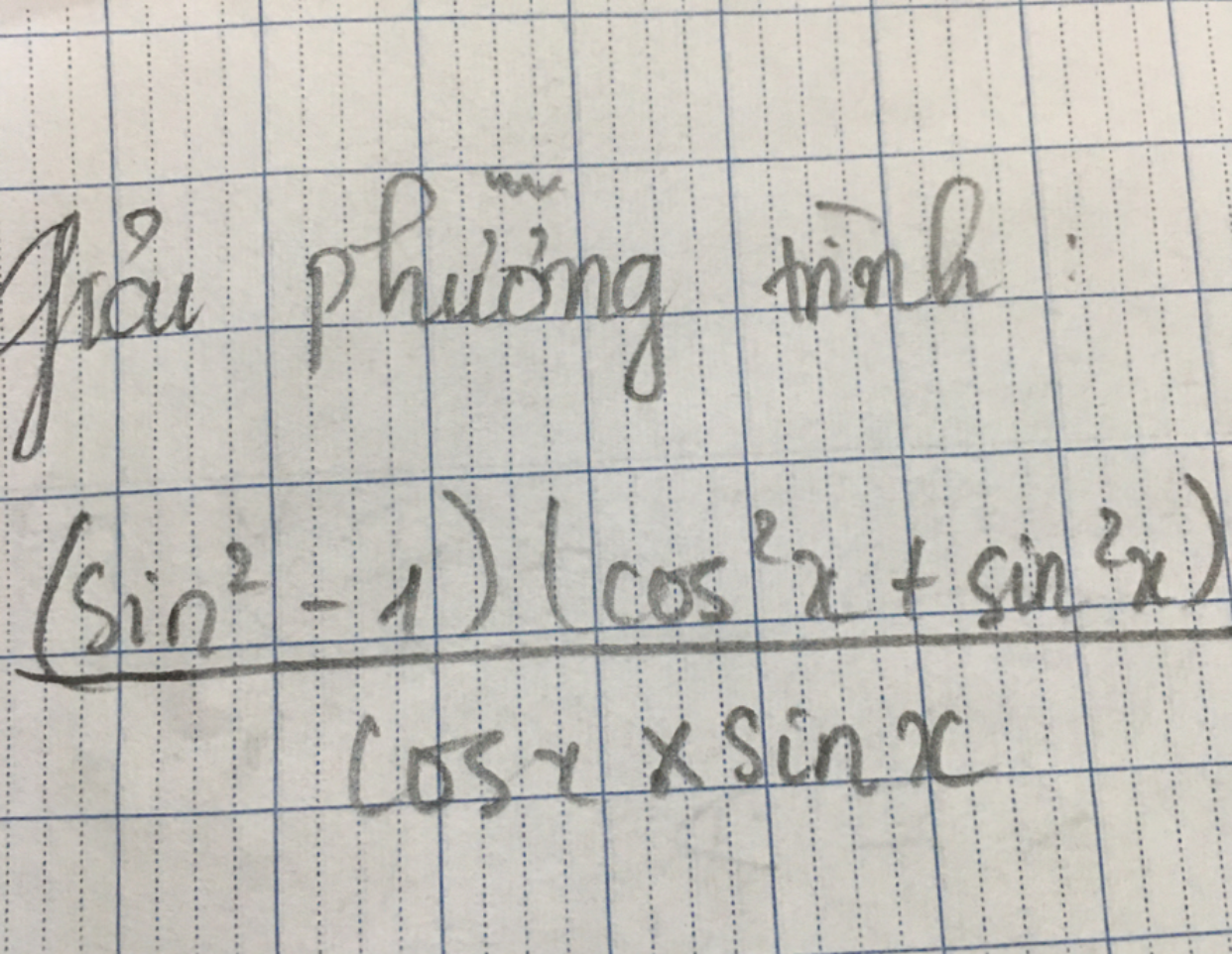 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

sin(2x + pi/12)cos(2x+pi/12) - 3cos(x-pi/6)+1=0
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 10sinxcosx 12= 12( sinx - cosxTheo dõi (0) 1 Trả lời
10sinxcosx 12= 12( sinx - cosxTheo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.28 trang 38 SBT Toán 11
Bài tập 1.29 trang 38 SBT Toán 11
Bài tập 1.31 trang 38 SBT Toán 11
Bài tập 1.32 trang 38 SBT Toán 11
Bài tập 1.33 trang 38 SBT Toán 11
Bài tập 1.34 trang 38 SBT Toán 11
Bài tập 1.35 trang 39 SBT Toán 11
Bài tập 1.38 trang 39 SBT Toán 11
Bài tập 1.36 trang 39 SBT Toán 11
Bài tập 1.37 trang 39 SBT Toán 11
Bài tập 27 trang 41 SGK Toán 11 NC
Bài tập 28 trang 41 SGK Toán 11 NC
Bài tập 29 trang 41 SGK Toán 11 NC
Bài tập 30 trang 41 SGK Toán 11 NC
Bài tập 31 trang 42 SGK Toán 11 NC
Bài tập 32 trang 42 SGK Toán 11 NC
Bài tập 33 trang 42 SGK Toán 11 NC
Bài tập 34 trang 42 SGK Toán 11 NC
Bài tập 35 trang 42 SGK Toán 11 NC
Bài tập 36 trang 42 SGK Toán 11 NC
Bài tập 37 trang 46 SGK Toán 11 NC
Bài tập 38 trang 46 SGK Toán 11 NC
Bài tập 39 trang 46 SGK Toán 11
Bài tập 40 trang 46 SGK Toán 11 NC






