Bài tập 37 trang 46 SGK Toán 11 NC
Mùa xuân ở Hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động qua lại vị trí cân bằng. Nghiên cứu trò chơi này, người ta thấy khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng (h. 1.32) được biểu diễn qua thời gian t (t ≥ 0 và được tính bằng giây) bởi hệ thức h = |d| với \(d = 3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right]\), trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp trái lại.
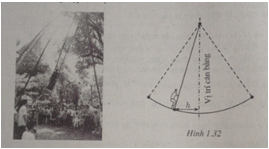
a. Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.
b. Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu cách vị trí cân bằng 2 mét (tính chính xác đến \(\frac{1}{{100}}\) giây).
Hướng dẫn giải chi tiết
a) Người chơi đu ở xa vị trí cân bằng nhất khi:
\(\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \pm 1\)
Ta có:
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \pm 1\\
\Leftrightarrow \sin \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = 0
\end{array}\\
\begin{array}{l}
\Leftrightarrow \frac{\pi }{3}\left( {2t - 1} \right) = k\pi \\
\Leftrightarrow t = \frac{1}{2}\left( {3k + 1} \right)
\end{array}
\end{array}\)
Ta cần tìm k nguyên để 0 ≤ t ≤ 2
\(\begin{array}{l}
0 \le t \le 2 \Leftrightarrow 0 \le \frac{1}{2}\left( {3k + 1} \right) \le 2\\
\Leftrightarrow - \frac{1}{3} \le k \le 1 \Leftrightarrow k \in \left\{ {0;1} \right\}
\end{array}\)
Với k= 0 thì \(t = \frac{1}{2}\). Với k = 1 thì t = 2.
Vậy trong 2 giây đầu tiên, người chơi đu ở xa vị trí cân bằng nhất vào các thời điểm \( \frac{1}{2}\) giây và 2 giây.
b)
Người chơi đu cách vị trí cân bằng 2 mét khi:
\(3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \pm 2\)
Ta có:
\(\begin{array}{l}
3\cos \left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \pm 2\\
\Leftrightarrow {\cos ^2}\left[ {\frac{\pi }{3}\left( {2t - 1} \right)} \right] = \frac{4}{9}\\
\Leftrightarrow 1 + \cos \left[ {\frac{{2\pi }}{3}\left( {2t - 1} \right)} \right] = \frac{9}{8}\\
\Leftrightarrow \cos \left[ {\frac{{2\pi }}{3}\left( {2t - 1} \right)} \right] = - \frac{1}{9}\\
\Leftrightarrow \frac{{2\pi }}{3}\left( {2t - 1} \right) = \pm \alpha + k2\pi \\
\Leftrightarrow t = \pm \frac{{3\alpha }}{{4\pi }} + \frac{1}{2} + \frac{{3k}}{2}
\end{array}\)
với \(\cos \alpha = - \frac{1}{9}\)
Ta tìm k nguyên để 0 ≤ t ≤ 2
- Với \(t = \frac{{3\alpha }}{{4\pi }} + \frac{1}{2} + \frac{{3k}}{2}\), ta có:
\(0 \le t \le 2 \Leftrightarrow - \frac{1}{3} - \frac{\alpha }{{2\pi }} \le k \le 1 - \frac{\alpha }{{2\pi }}\)
Với \(\cos \alpha = - \frac{1}{9}\) ta chọn \(\alpha \approx 1,682\)
Khi đó \( - 0,601 < k < 0,732\) suy ra k = 0 và \(t \approx 0,90\)
- Với \(t = - \frac{{3\alpha }}{{4\pi }} + \frac{1}{2} + \frac{{3k}}{2}\), ta có:
\(0 \le t \le 2 \Leftrightarrow - \frac{1}{3} + \frac{\alpha }{{2\pi }} \le k \le 1 + \frac{\alpha }{{2\pi }}\)
Vì \(\alpha \approx 1,682\) nên \( - 0,066 < k < 1,267\) suy ra \(k \in \left\{ {0;1} \right\}\)
Với k = 0, ta có \(t \approx 0,10\); với k = 1, ta có \(t \approx 1,60\)
Kết luận: Trong khoảng 2 giây đầu tiên, có ba thời điểm mà người chơi đu cách vị trí cân bằng 2 mét, đó là \(t \approx 0,10\) giây; \(t \approx 0,90\) giây và \(t \approx 1,60\) giây.
-- Mod Toán 11 HỌC247
-


Em sẽ rất biết ơn ai giải giúp em bài này!
Giải phương trình: \((2sinx+1)(3cos4x+2sinx-4)+4cos^2x=3\)
Theo dõi (0) 1 Trả lời -


Giải Phương trình: \(cosx + sinx - cos3x=0\)
bởi minh thuận
 08/02/2017
08/02/2017
Hôm qua làm kiểm tra 1 tiết Toán, mình giải không biết đúng hay sai nữa!
Giải Phương trình: \(cosx + sinx - cos3x=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình \(\sqrt{2}sin2x=2cosx+1-\sqrt{2}sinx\)
bởi hà trang
 06/02/2017
06/02/2017
Mình giải ra đáp số rồi mà không biết đúng hay sai nữa, khó quá.
Giải phương trình \(\sqrt{2}sin2x=2cosx+1-\sqrt{2}sinx\)
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(sin2x+2cosx-sinx-1=0\)
bởi Mai Thuy
 07/02/2017
07/02/2017
Khó quá, em bỏ cuộc rồi, mọi người giúp vs! Em cảm ơn nhiều ạ.
Giải phương trình: \(sin2x+2cosx-sinx-1=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình \(sinx=1-\sqrt{3}cosx\)
bởi Lê Tường Vy
 07/02/2017
07/02/2017
Làm toát mồ hôi mà vẫn không ra, giúp em vs!
Giải phương trình \(sinx=1-\sqrt{3}cosx\)
Theo dõi (0) 1 Trả lời -


Bài này phải làm sao mọi người?
Giải phương trình sau trên tập số thực:
\(sin2x-2\sqrt{3}cos^2x=0\) với \(x\in (0;\frac{3\pi}{2})\)Theo dõi (0) 1 Trả lời -


Giải PT sau:
\(cosx.cos\frac{x}{2}.cos\frac{3x}{2}-sinx.sin\frac{x}{2}.sin\frac{3x}{2}=\frac{1}{2}\)
Theo dõi (0) 0 Trả lời -


Giải phương trình: \(sin2x-\sqrt{3}cosx=0\)
bởi Nguyễn Phương Khanh
 06/02/2017
06/02/2017
Khó quá, em bỏ cuộc rồi, mọi người giúp vs! Em cảm ơn nhiều ạ.
Giải phương trình: \(sin2x-\sqrt{3}cosx=0\)
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\cos 2x = 5\cos x - 3\)
bởi Nguyễn Sơn Ca
 07/02/2017
07/02/2017
Hôm qua làm kiểm tra 1 tiết Toán, mình giải không biết đúng hay sai nữa!
Giải phương trình: \(\cos 2x = 5\cos x - 3\).
Theo dõi (0) 1 Trả lời -


Bài này phải làm sao mọi người?
Giải phương trình \(2sin(2x+\frac{\pi}{3})-\sqrt{3}cos2x=1\)
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2sinx+sin2x=2cos^2\frac{x}{2}\)
bởi Nhat nheo
 08/02/2017
08/02/2017
Hôm qua làm kiểm tra 1 tiết Toán, mình giải không biết đúng hay sai nữa!
Giải phương trình: \(2sinx+sin2x=2cos^2\frac{x}{2}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(\sqrt{3}sin2x+cos2x=sinx-\sqrt{3}cosx\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f(x)=2\sqrt{3}sinx-cos2x+5\). Giải phương trình f'(x) = 0
Theo dõi (0) 1 Trả lời -


bởi Long lanh
 08/02/2017
08/02/2017
a. Gọi z1, z2 là các nghiệm phức của phương trình \(z^2-6z+13=0\). Tính \(\left | z_1-z_2 \right |\)
b. Giải phương trình \(4.9^{x+1}-13.6^{x+1}+9.4^{x+1}=0\)Theo dõi (0) 1 Trả lời -


Giải PT (sinx+3cosx+2)(1-2cosx)=4sin^2x-3
bởi Tran Hai
 27/07/2017
27/07/2017
(sinx+3cosx+2)(1-2cosx)=4sin2x-3
Theo dõi (0) 2 Trả lời





