Bài tập 31 trang 42 SGK Toán 11 NC
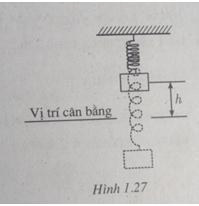
Một vật nặng treo bởi một chiếc lò xo chuyển động lên xuống qua vị trí cân bằng. Khoảng cách h từ vật đó đến vị trí cân bằng ở thời điểm t giây được tính theo công thức h = |d| trong đó d = 5sin6t–4cos6t với d được tính bằng xentimet, ta quy ước rằng d > 0 khi vật ở phía trên vị trí cân bằng, d < 0 khi vật ở phía dưới vị trí cân bằng. Hỏi:
a. Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng?
b. Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất?
(Tính chính xác đến \(\frac{1}{{100}}\) giây).
Hướng dẫn giải chi tiết
Ta có
\(\begin{array}{l}
5\sin 6t - 4\cos 6t\\
= \sqrt {41} \left( {\frac{5}{{\sqrt {41} }}\sin 6t - \frac{4}{{\sqrt {41} }}\cos 6t} \right)\\
= \sqrt {41} \sin \left( {6t - \alpha } \right)
\end{array}\)
trong đó số α được chọn sao cho \(\cos \alpha = \frac{5}{{\sqrt {41} }}\) và \(\sin \alpha = \frac{4}{{\sqrt {41} }}\).
Sử dụng bảng số hoặc máy tính bỏ túi, ta chọn được \(\alpha \approx 0,675\).
a) Vật ở vị trí cân bằng khi d = 0, nghĩa là sin(6t–α) = 0
\( \Leftrightarrow t = \frac{\alpha }{6} + k\frac{\pi }{6},k \in Z\)
Ta cần tìm k nguyên dương sao cho 0 ≤ t ≤ 1
\(\begin{array}{l}
0 \le t \le 1 \Leftrightarrow 0 \le \frac{\alpha }{6} + k\frac{\pi }{6} \le 1\\
\Leftrightarrow - \frac{\alpha }{\pi } \le k \le \frac{{6 - \alpha }}{\pi }
\end{array}\)
Với \(\alpha \approx 0,675\), ta thu được −0,215 < k < 1,7 nghĩa là \(k \in \left\{ {0;1} \right\}\). Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở vị trí cân bằng là:
\(t \approx \frac{\alpha }{6} \approx 0,11\) (giây) và \(t = \frac{\alpha }{6} + \frac{\pi }{6} \approx 0,64\) (giây)
b) Vật ở xa vị trí cân bằng nhất khi và chỉ khi |d| nhận giá trị lớn nhất.
Điều đó xảy ra nếu sin(6t–α) = ±1. Ta có:
\(\begin{array}{l}
\sin \left( {6t - \alpha } \right) = \pm 1 \Leftrightarrow \cos \left( {6t - \alpha } \right) = 0\\
\Leftrightarrow t = \frac{\alpha }{6} + \frac{\pi }{{12}} + k\frac{\pi }{6}
\end{array}\)
Ta tìm k nguyên dương sao cho 0 ≤ t ≤ 1
\(\begin{array}{*{20}{l}}
{0 \le t \le 1 \Leftrightarrow 0 \le \frac{\alpha }{6} + \frac{\pi }{{12}} + k\frac{\pi }{6} \le 1}\\
{ \Leftrightarrow - \frac{\alpha }{\pi } - \frac{1}{2} \le k \le \frac{{6 - \alpha }}{\pi } - \frac{1}{2}}
\end{array}\)
Với \(\alpha \approx 0,675\), ta thu được −0,715 < k < 1,2; nghĩa là k ∈ {0;1}.
Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất là:
\(t = \frac{\alpha }{6} + \frac{\pi }{{12}} \approx 0,37\) (giây)
và \(t = \frac{\alpha }{6} + \frac{\pi }{{12}} + \frac{\pi }{6} \approx 0,90\) (giây)
-- Mod Toán 11 HỌC247
-


Giải phương trình 1+2cos2x=sin2x
bởi Anh Nguyễn
 01/11/2018
01/11/2018
Giải 1+2cos2x=sin2x
Theo dõi (0) 1 Trả lời -


giải pt
\(2\sin\left(2x+\frac{9\pi}{4}\right)+7\sqrt{2}\sin x+\sqrt{2}\sin\left(x+\frac{11\pi}{2}\right)=4\sqrt{2}\)
Theo dõi (0) 1 Trả lời -


Giải phương trình cosx - sinx + 6sinxcosx = 1
bởi My Le
 01/11/2018
01/11/2018
cosx - sinx + 6sinxcosx = 1
Theo dõi (0) 1 Trả lời -


Giải phương trình cos^2 2x.sin^2 2=0
bởi thanh hằng
 25/09/2018
25/09/2018
cos^2 2x . sin^2 x=0
Theo dõi (0) 1 Trả lời -


Giải pt sin4x.sin7x=cos3x.cos6x
bởi Tuấn Huy
 25/09/2018
25/09/2018
Giải Phương Trình: sin4x.sin7x=cos3x.cos6x
Ai biết giải giúp nha!!!!
Theo dõi (0) 1 Trả lời -


Giải phương trình sinx+cosx+3sinx.cosx-1=0
bởi Hương Lan
 01/11/2018
01/11/2018
sinx+cosx+3sinxcosx-1=0
Theo dõi (0) 1 Trả lời -


Giải phương trình 2sin2x + căn 2 sin4x = 0
bởi Nguyễn Thanh Thảo
 06/11/2018
06/11/2018
2sin2x + căn 2 sin4x = 0
Theo dõi (0) 2 Trả lời -


Giải phương trình (3sin2x-2sinx)/(sin2xcosx)=2
bởi Việt Long
 25/09/2018
25/09/2018
Giải phương trình :
\(\frac{3\sin2x-2\sin x}{\sin2x\cos x}=2\)
Theo dõi (0) 1 Trả lời -


Giải phương trình :
\(2\sin6x-2\sin4x+\sqrt{3}\cos2x=\sqrt{3}+\sin2x\)
Theo dõi (0) 1 Trả lời -


Giải phương trình cosx-căn 3sinx=căn2
bởi Nguyễn Thủy
 25/09/2018
25/09/2018
Giải các phương trình sau:
a) cosx - √3sinx = √2; b) 3sin3x - 4cos3x = 5;
b) 2sin2x + 2cos2x - √2 = 0; c) 5cos2x + 12sin2x -13 = 0.
Theo dõi (0) 1 Trả lời -


Giải phương trình 6sin^2x + 2sin^2 2x =5
bởi cuc trang
 25/09/2018
25/09/2018
6sin^2x + 2sin^2 2x =5
Theo dõi (0) 1 Trả lời -


Giải pt 4cos^2x+3 căn 2sin2x=8cosx
bởi Bin Nguyễn
 24/10/2018
24/10/2018
32, giai
\(4cos^2x+3\sqrt{2}sin2x=8cosx\)
Theo dõi (0) 1 Trả lời -


Giải phương trình 1+sinx+cosx+sin2x+cos2x=0
bởi Nguyen Ngoc
 01/11/2018
01/11/2018
6. giai pt
1+sinx+cosx+sin2x+cos2x=0
Theo dõi (0) 2 Trả lời -


Giải phương trình sin2x-cos2x+5sinx-cosx-2=0
bởi Sasu ka
 01/11/2018
01/11/2018
Giải phương trình sin2x-cos2x+5sinx-cosx-2=0
Theo dõi (0) 1 Trả lời -


Giải phương trình 2sin^2x+sin2x+căn 2*sin(x-pi/4)
bởi Tram Anh
 25/09/2018
25/09/2018
Giải phương trình :
\(2\sin^2x+\sin2x+\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)=1\)
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 29 trang 41 SGK Toán 11 NC
Bài tập 30 trang 41 SGK Toán 11 NC
Bài tập 32 trang 42 SGK Toán 11 NC
Bài tập 33 trang 42 SGK Toán 11 NC
Bài tập 34 trang 42 SGK Toán 11 NC
Bài tập 35 trang 42 SGK Toán 11 NC
Bài tập 36 trang 42 SGK Toán 11 NC
Bài tập 37 trang 46 SGK Toán 11 NC
Bài tập 38 trang 46 SGK Toán 11 NC
Bài tập 39 trang 46 SGK Toán 11
Bài tập 40 trang 46 SGK Toán 11 NC





