Toán 10 Kết nối tri thức Bài tập cuối chương 4

- Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

- Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

- Hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được gọi là bằng nhau, kí hiệu \(\overrightarrow a  = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.

a) Tổng của hai vectơ

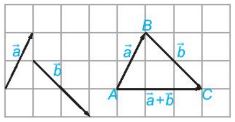
- Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tuỳ ý và vẽ \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b \) (Hình bên dưới). Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  + \overrightarrow b \). 

- Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

- Quy tắc ba điểm: Với ba điểm bắt kì A, B, C, ta có \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

- Quy tắc hình bình hành: Nếu ABCD là một hình binh hành thì \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) 

- Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:

• Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \)

• Tính chất kết hợp: \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)

• Tính chất của vectơ-không: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \) 

b) Hiệu của hai vectơ

- Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \). Vectơ đối của \(\overrightarrow a \) được kí hiệu là \(-\overrightarrow a \).

- Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó.

- Vectơ \(\overrightarrow a  + \left( { - \overrightarrow b } \right)\) được gọi là hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  - \overrightarrow b \). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

- Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  - \overrightarrow {OM} \)

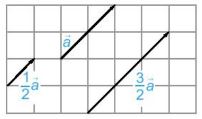
Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k > 0 là một vectơ, ki hiệu là \(k\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(k\left| {\overrightarrow a } \right|\).

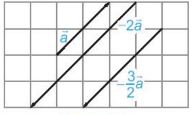
Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k <0 là một vectơ, ki hiệu là \(k\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(-k\left| {\overrightarrow a } \right|\).

- Các tính chất của phép nhân vectơ với một số

Với hai vectơ \(\overrightarrow a ,\overrightarrow b\) và hai số thực k, t, ta luôn có: 

\(\begin{array}{l}
*k\left( {t\overrightarrow a } \right) = \left( {kt} \right)\overrightarrow a \\
*\left( {k + t} \right)\overrightarrow a  = k\overrightarrow a  + t\overrightarrow a \\
*k\left( {\overrightarrow a  + \overrightarrow b } \right) = k\overrightarrow a  + k\overrightarrow b ;\left( {\overrightarrow a  - \overrightarrow b } \right) = k\overrightarrow a  - k\overrightarrow b .\\
*1\overrightarrow a  = \overrightarrow a ;\left( { - 1} \right)\overrightarrow a  =  - \overrightarrow a 
\end{array}\)

a) Tọa độ của vectơ

Với mỗi vectơ ứ trên mặt phẳng Oxy, có duy nhất cặp số \(\left( {{x_0};{y_0}} \right)\) sao cho \(\overrightarrow u  = {x_0}\overrightarrow i  + {y_0}\overrightarrow j \). Ta nói vectơ \(\overrightarrow u \) có toạ độ \(\left( {{x_0};{y_0}} \right)\) và viết \(\overrightarrow u  = \left( {{x_0};{y_0}} \right)\) hay \(\overrightarrow u \left( {{x_0};{y_0}} \right)\). Các số \({{x_0},{y_0}}\) tương ứng được gọi là hoành độ, tung độ của \(\overrightarrow u \).

b) Biểu thức tọa độ của các phép toán vectơ

- Cho hai vectơ \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {x;y} \right)\). Khi đó:

\(\begin{array}{*{20}{l}}
{*\vec u + \vec v = \left( {x + x';y + y'} \right);}\\
{*\vec u - \vec v = \left( {x - x';y - y'} \right);}\\
{*k\vec u = \left( {kx;ky} \right),k \in R}
\end{array}\)

- Nếu điểm M có toạ độ (x; y) thì vecto \(\overrightarrow {OM} \) có toạ độ (x; y) và độ dài \(\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}} \).

- Với hai điểm M(x; y) và N(x'; y') thì \(\overrightarrow {MN}  = \left( {x' - x;y' - y} \right)\) và khoảng cách giữa hai điểm M, N là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x' - x} \right)}^2} + {{\left( {y' - y} \right)}^2}} \) 

a) Góc giữa hai vectơ

Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác \({\vec 0}\). Từ một điểm A tuỳ ý, vẽ các vectơ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \) (Hình cho bên dưới). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay đơn giản là góc giữa hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) kí hiệu là \(\left( {\overrightarrow u ,\overrightarrow v } \right)\).

b) Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u .\overrightarrow v \), được xác định bởi công thức sau:

\(\overrightarrow u .\overrightarrow v  = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.cos\left( {\overrightarrow u ,\overrightarrow v } \right)\) 

c) Biểu thức tọa độ và tính chất của tích vô hướng

Tích vô hướng của hai vectơ \(\overrightarrow u  = \left( {x';y'} \right)\) được tính theo công thức: \(\overrightarrow u .\overrightarrow v  = xx' + yy'\)

Tính chất của tích vô hướng 

Với ba vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}} \) bất kì và mọi số thực k. ta có:

* \(\overrightarrow u .\overrightarrow v  = \overrightarrow v .\overrightarrow u \) (tính chất giao hoán);

* \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow {\rm{w}} } \right) = \overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow {\rm{w}} \) (tính chất phân phối đối với phép cộng);

* \(\left( {k\overrightarrow u } \right).\overrightarrow v  = k\left( {\overrightarrow u .\overrightarrow v } \right) = \overrightarrow u \left( {k.\overrightarrow v } \right)\). 

Câu 1: Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)

Hướng dẫn giải

Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD}  = \overrightarrow {BC} \).

Do đó \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \).

Câu 2: Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u  = (2; - 3),\;\overrightarrow v  = (4;1),\;\overrightarrow a  = (8; - 12)\)

a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\;\overrightarrow v ,\;\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)

b) Tìm tọa độ của các vectơ \(\overrightarrow u  + \;\overrightarrow v ,\;4.\;\overrightarrow u \)

c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\;\overrightarrow a \)

Hướng dẫn giải

a) Ta có: \(\overrightarrow u  = (2; - 3)\)

\( \Rightarrow \overrightarrow u  = 2.\;\overrightarrow i  + \left( { - 3} \right).\;\overrightarrow j \)

Tương tự ta có: \(\overrightarrow v  = (4;1),\;\overrightarrow a  = (8; - 12)\)

\( \Rightarrow \overrightarrow v  = 4.\;\overrightarrow i  + 1.\;\overrightarrow j ;\;\;\overrightarrow a  = 8.\;\overrightarrow i  + \left( { - 12} \right).\;\overrightarrow j \)

b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u  = 2.\;\overrightarrow i  + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v  = 4.\;\overrightarrow i  + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u  + \;\overrightarrow v  = \left( {2.\;\overrightarrow i  + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i  + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u  = 4\left( {2.\;\overrightarrow i  + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u  + \;\overrightarrow v  = \left( {2.\;\overrightarrow i  + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j  + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u  = 4.2.\;\overrightarrow i  + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u  + \;\overrightarrow v  = 6.\;\overrightarrow i  + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u  = 8.\;\overrightarrow i  + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)

c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u  = 8.\;\overrightarrow i  + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a  = 8.\;\overrightarrow i  + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u  = \overrightarrow a \)

Câu 3: Xét các vectơ cùng phương trong hình cho sau. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).

Hướng dẫn giải

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.

Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.

Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.

Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.

Qua bài giảng này giúp các em ôn tập lại các kiến thức sau:

- Hai vectơ cùng phương, cùng hướng, bằng nhau

- Tổng và hiệu của hai vectơ

- Tích của một vectơ với một số

- Vectơ trong mặt phẳng tọa độ

- Tích vô hướng của hai vectơ

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Kết nối tri thức Bài tập cuối chương 4 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Cho ba điểm A, B, C phân biệt. Khi đó khẳng định nào sau đây đúng nhất.

  • A. A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.
  • B. A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) cùng phương. 
  • C. A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \) cùng phương. 
  • D. Cả A, B, C đều đúng.

• Câu 2:

  Cho lục giác đều ABCDEF có tâm O. Đẳng thức nào sau đây sai?

  • A. \(\overrightarrow {AB}  = \overrightarrow {ED} \) 
  • B. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AF} } \right|\) 
  • C. \(\overrightarrow {OD}  = \overrightarrow {BC} \)
  • D. \(\overrightarrow {OB}  = \overrightarrow {OE} \) 

• Câu 3:

  Cho các điểm phân biệt A, B, C, D, E, F. Đẳng thức nào sau đây sai?

  • A. \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {EF}  = \overrightarrow {AF}  + \overrightarrow {ED}  + \overrightarrow {BC} \) 
  • B. \(\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {EF}  = \overrightarrow {AF}  + \overrightarrow {ED}  + \overrightarrow {CB} \) 
  • C. \(\overrightarrow {AE}  + \overrightarrow {BF}  + \overrightarrow {DC}  = \overrightarrow {DF}  + \overrightarrow {BE}  + \overrightarrow {AC} \) 
  • D. \(\overrightarrow {AC}  + \overrightarrow {BD}  + \overrightarrow {EF}  = \overrightarrow {AD}  + \overrightarrow {BF}  + \overrightarrow {EC} \) 

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 4 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Giải bài 4.27 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.28 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.29 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.30 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.31 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.32 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.33 trang 71 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.34 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.35 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.36 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.37 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.38 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.39 trang 72 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.39 trang 66 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.40 trang 66 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.41 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.42 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.43 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.44 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.45 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.46 trang 67 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.47 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.48 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.49 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.50 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.51 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.52 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.53 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.54 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.55 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.56 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.57 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.58 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.59 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.60 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.61 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.62 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.63 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.64 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.65 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.66 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.67 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.68 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.69 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 4.70 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!