Giải bài 4.55 trang 69 SBT Toán 10 Kết nối tri thức tập 1
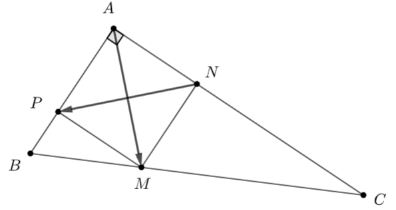
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 1,\,\,AC = 2.\) Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(2BM = MC,\,\,CN = 2NA,\,\,AP = 2PB.\) Giá trị của tích vô hướng \(\overrightarrow {AM} .\overrightarrow {NP} \) bằng
A. \(\frac{2}{3}\)
B. \( - \frac{1}{2}\)
C. \(0\)
D. \(1\)
Hướng dẫn giải chi tiết Bài 4.55
Phương pháp giải
Chứng minh: \(MN\)//\(AB\), \(MP\)//\(AC\) => tứ giác \(APMN\) là hình bình hành
Mặt khác \(\widehat {PAN} = {90^ \circ }\)
\( \Rightarrow \) tứ giác \(APMN\) là hình vuông
Lời giải chi tiết
Ta có: \(\frac{{CN}}{{CA}} = \frac{{CM}}{{CM}} = \frac{2}{3}\)
\( \Rightarrow \) \(MN\)//\(AB\) hay \(MN\)//\(AP\) (1)
Ta có: \(\frac{{BP}}{{BA}} = \frac{{BM}}{{BC}} = \frac{1}{3}\)
\( \Rightarrow \) \(MP\)//\(AC\) hay \(MP\)//\(AN\) (2)
Ta có: \(AP = \frac{2}{3}AB = \frac{2}{3}.1 = \frac{2}{3}\) và \(AN = \frac{1}{3}AC = \frac{2}{3}\)
Từ (1) và (2) \( \Rightarrow \) tứ giác \(APMN\) là hình bình hành
Mặt khác \(\widehat {PAN} = {90^ \circ }\) và \(AP = AN = \frac{2}{3}\)
\( \Rightarrow \) tứ giác \(APMN\) là hình vuông
\( \Rightarrow \) \(AM \bot PN\) \( \Rightarrow \overrightarrow {AM} .\overrightarrow {NP} = 0\)
Chọn C.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 4.53 trang 68 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.54 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.56 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.57 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.58 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.59 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.60 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.61 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.62 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.63 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.64 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.65 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.66 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.67 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.68 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.69 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.70 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT