Giải bài 4.56 trang 69 SBT Toán 10 Kết nối tri thức tập 1
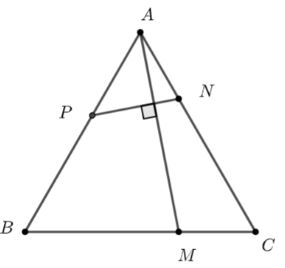
Cho tam giác \(ABC\) đều các cạnh có độ dài bằng 1. Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(BM = 2MC,\,\,CN = 2NA\) và \(AM \bot NP.\) Tỉ số của \(\frac{{AP}}{{AB}}\) bằng
A. \(\frac{5}{{12}}\)
B. \(\frac{7}{{12}}\)
C. \(\frac{5}{7}\)
D. \(\frac{7}{5}\)
Hướng dẫn giải chi tiết Bài 56
Phương pháp giải
- Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
- Biểu diễn các vectơ \(\overrightarrow {PN} \) và \(\overrightarrow {AM} \) theo các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)
- Tìm x dựa vào tích vô hướng của hai vectơ \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
Lời giải chi tiết
Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
Ta có: \(\overrightarrow {PN} = \overrightarrow {PA} + \overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} \)
Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
Ta có: \(AM \bot PN\) \( \Rightarrow \) \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
\( \Leftrightarrow \) \(\left( {\frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right).\left( {\frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}\overrightarrow {AB} .\overrightarrow {AC} - \frac{x}{3}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{{2x}}{3}\overrightarrow {AC} .\overrightarrow {AB} = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}.\frac{1}{2} - \frac{x}{3} + \frac{2}{9} - \frac{{2x}}{3}.\frac{1}{2} = 0\)
\( \Leftrightarrow \) \(\frac{1}{{18}} - \frac{x}{3} + \frac{2}{9} - \frac{x}{3} = 0\)
\( \Leftrightarrow \) \(1 - 6x + 4 - 6x = 0\)
\( \Leftrightarrow \) \(12x = 5\) \( \Leftrightarrow \) \(x = \frac{5}{{12}}\)
Vậy \(\frac{{AP}}{{AB}} = \frac{5}{{12}}\)
Chọn A.
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Giải bài 4.54 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.55 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.57 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.58 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.59 trang 69 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.60 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.61 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.62 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.63 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.64 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.65 trang 70 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.66 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.67 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.68 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.69 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.70 trang 71 SBT Toán 10 Kết nối tri thức tập 1 - KNTT