HỌC247 xin giới thiệu đến các em học sinh lớp 10 Bài Tổng và hiệu của hai vectơ. Bài giảng có lý thuyết được tóm tắt ngắn gọn và các bài tập minh hoạ kèm theo lời giải chi tiết cho các em tham khảo, rèn luyện kỹ năng giải Toán 10. Mời các em học sinh cùng tham khảo.
Tóm tắt lý thuyết
1.1. Tổng của hai vectơ
|
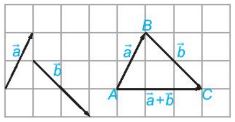
Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tuỳ ý và vẽ \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \) (Hình bên dưới). Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a + \overrightarrow b \). Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ. |
|---|
- Quy tắc ba điểm: Với ba điểm bắt kì A, B, C, ta có \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
- Quy tắc hình bình hành: Nếu ABCD là một hình binh hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
- Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:
- Tính chất giao hoán: \(\overrightarrow a + \overrightarrow b = \overrightarrow b + \overrightarrow a \)
- Tính chất kết hợp: \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c = \overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\)
- Tính chất của vectơ-không: \(\overrightarrow a + \overrightarrow 0 = \overrightarrow 0 + \overrightarrow a = \overrightarrow a \)
Chú ý: Do các vectơ \(\left( {\overrightarrow a + \overrightarrow b } \right) + \overrightarrow c \) và \(\overrightarrow a + \left( {\overrightarrow b + \overrightarrow c } \right)\) bằng nhau, nên ta còn viết chúng dưới dạng \(\overrightarrow a + \overrightarrow b + \overrightarrow c \) và gọi là tổng cửa ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \). Tương tự, ta cũng có thể viết tổng của một số vectơ mà không cần dùng các dấu ngoặc.
Ví dụ: Cho hình Vuông ABCD với cạnh có độ dài bằng 1. Tính độ dài của các vectơ \(\overrightarrow {AB} + \overrightarrow {CB} ,\overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} \).
Giải
Do \(\overrightarrow {AB} = \overrightarrow {DC} \) nên \(\overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB} \)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
Ta có \(\overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} = \left( {\overrightarrow {AB} + \overrightarrow {BD} } \right) + \overrightarrow {DC} = \overrightarrow {AD} + \overrightarrow {DC} = \overrightarrow {AC} \)
Do đó \(\left| {\overrightarrow {AB} + \overrightarrow {DC} + \overrightarrow {BD} } \right| = AC = \sqrt 2 \)
1.2. Hiệu của hai vectơ
|
- Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \). Vectơ đối của \(\overrightarrow a \) được kí hiệu là \(-\overrightarrow a \). - Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó. |
|---|
Chú ý: Hai vectơ đối nhau khi và chỉ khi tổng của chúng bằng \(\overrightarrow 0 \).
| - Vectơ \(\overrightarrow a + \left( { - \overrightarrow b } \right)\) được gọi là hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a - \overrightarrow b \). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ. |
|---|
Chú ý: Nếu \(\overrightarrow b + \overrightarrow c = \overrightarrow a \) thì \(\overrightarrow a - \overrightarrow b = \overrightarrow a + \left( { - \overrightarrow b } \right) = \overrightarrow c + \overrightarrow b + \left( { - \overrightarrow b } \right) = \overrightarrow c + \overrightarrow 0 = \overrightarrow c \)
Với ba điểm O, M, N tuỷ ý, ta có \(\overrightarrow {MN} = \overrightarrow {MO} + \overrightarrow {ON} = \left( { - \overrightarrow {OM} } \right) + \overrightarrow {ON} = \overrightarrow {ON} - \overrightarrow {OM} \)
- Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \)
Ví dụ: Cho hình bình hành ABCD và một điểm O bất kì.
Chứng minh rằng \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \)
Giải
Áp dụng quy tắc hiệu, ta có \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {AB} ,\overrightarrow {OC} - \overrightarrow {OD} = \overrightarrow {DC} \)
Mặt khác \(\overrightarrow {AB} = \overrightarrow {DC} \) nên \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \)
Chú ý: Phép cộng vectơ tương ứng với các quy tắc tổng hợp lực, tổng hợp vận tốc:
+ Nếu hai lực cùng tác động vào chất điểm A và được biểu diễn bởi các vectơ \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) thì hợp lực tác động vào A được biểu diễn bởi vectơ \(\overrightarrow {{u_1}} + \overrightarrow {{u_2}} \)
+ Nếu một con thuyền dĩ chuyển trên sông với vận tốc riêng (vận tốc so với dòng nước) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}} \) và vận tốc của dòng nước (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_n}} \) thì vận tốc thực tế của thuyền (so với bờ) được biểu diễn bởi vectơ \(\overrightarrow {{v_r}} + \overrightarrow {{v_n}} \).
Bài tập minh họa
Câu 1:
Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?
Hướng dẫn giải
Gọi: vận tốc thực tế của tàu là \(\overrightarrow v \)
Vận tốc riêng của tàu (đối với dòng nước) là \(\overrightarrow {{v_t}} \)
Vận tốc của dòng nước (đối với bờ) là \(\overrightarrow {{v_n}} \)
Ta có: \(\overrightarrow v = \overrightarrow {{v_n}} + \overrightarrow {{v_t}} \)
Để tàu sang bờ bên kia nhanh nhất thì vận tốc thực tế của tàu có hướng vuông góc với bờ.
Thao quy tắc hình bình hành thì \(\overrightarrow v \) là vecto đường chéo xuất phát từ gốc chung của vecto vận tốc riêng của tàu và vecto vận tốc dòng nước tác động lên tàu.
Câu 2: Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \)
Hướng dẫn giải
Vì ABCD là hình bình hành nên \(\left\{ \begin{array}{l}AD//\;BC\\AD = BC\end{array} \right.\), hay \(\overrightarrow {AD} = \overrightarrow {BC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Luyện tập Bài 8 Toán 10 KNTT
Qua bài giảng trên sẽ giúp các em nắm được các nội dung như sau:
- Nắm được cách dựng vectơ tổng của hai vectơ theo định nghĩa và theo quy tắc hình bình hành.
- Nắm các tính chất của phép cộng vectơ , liên hệ với phép cộng hai số thực.
3.1. Bài tập trắc nghiệm Bài 8 Toán 10 KNTT
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Kết nối tri thức Chương 4 Bài 8 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. \(\overrightarrow {AM} \)
- B. \(\overrightarrow {PB} \)
- C. \(\overrightarrow {AP} \)
- D. \(\overrightarrow {MN} \)
-
- A. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 2 \)
- B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{{a\sqrt 2 }}{2}\)
- C. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a\)
- D. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\)
-
- A. \(\left| {\overrightarrow {CA} + \overrightarrow {AB} } \right| = 2\)
- B. \(\left| {\overrightarrow {CA} + \overrightarrow {AB} } \right| = 2\sqrt {13} \)
- C. \(\left| {\overrightarrow {CA} + \overrightarrow {AB} } \right| = 5\)
- D. \(\left| {\overrightarrow {CA} + \overrightarrow {AB} } \right| = \sqrt {13} \)
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 8 Toán 10 KNTT
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Kết nối tri thức Chương 4 Bài 8 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động 1 trang 51 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 2 trang 51 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 3 trang 52 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Luyện tập 1 trang 52 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Hoạt động 4 trang 52 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Luyện tập 2 trang 53 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Vận dụng trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.6 trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.7 trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.8 trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.9 trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.10 trang 54 SGK Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.7 trang 50 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.8 trang 50 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.9 trang 50 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.10 trang 51 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.11 trang 51 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Giải bài 4.12 trang 51 SBT Toán 10 Kết nối tri thức tập 1 - KNTT
Hỏi đáp Bài 8 Toán 10 KNTT
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 10 HỌC247


.JPG)
.JPG)
(1).JPG)
(1).JPG)





