Giải bài 46 tr 46 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC.\) Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đường thẳng \(AB, BC, CA\) là bằng nhau, đồng thời khoảng cách này là ngắn nhất.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
+) Một điểm nằm trong góc và cách đều hai cạnh của một góc thì nằm trên tia phân giác của góc đó.
Lời giải chi tiết
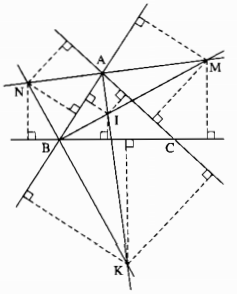
Nếu O là điểm nằm trong ∆ABC
Kẻ \(OH \bot AB,OK \bot BC,OI \bot {\rm{A}}C\)
Vì điểm O cách đều các đường thẳng AB, BC, CA.
\( \Rightarrow \) OH = OK = OI
OH = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ABC}\)
OI = OK
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {ACB}\)
Vậy O là giao điểm các đường phân giác của ∆ABC.
Nếu O’ nằm ngoài ∆ABC
Kẻ \(O'D \bot AB,O'E \bot BC,O'F \bot {\rm{AC}}\)
\( \Rightarrow \) O'D = O'E = O'F
O'D = O'F
\( \Rightarrow \) O nằm trên tia phân giác \(\widehat {BAC}\)
O’D = O’E
\( \Rightarrow \) O’ nằm trên tia phân giác \(\widehat {DBC}\)
\( \Rightarrow \) O’ là giao điểm phân giác trong của \(\widehat {BAC}\) và phân giác ngoài tại đỉnh D. nên A, O, O’ thẳng; A, H, D thẳng hàng.
Ta có: OH < O’D
Vậy O là giao điểm các đường phân giác trong của ∆ABC cách đều ba đường thẳng AB, BC, CA và ngắn nhất.
-- Mod Toán 7 HỌC247
-


cho tam giác ABC. Tia phân giác của B VÀ C cắt nhau tại I. Từ I kẻ đường thẳng song song với ab, cắt AC và BC tại D và E
CMR: DE=AD+BE
Theo dõi (0) 1 Trả lời -


Tam giác ABC cân ở A có AB=5cm, BC=8cm. Đường phân giác AD cắt đường trung tuyến BM ở I.
a) Chứng minh ADB=90° và tính BD.
b) Tính độ dài AD, AI.
Theo dõi (0) 1 Trả lời -


Tính góc BIC biết tam giác ABC có góc A=78 độ, I là giao điểm của 2 tia phân giác góc B, C
bởi thanh hằng
 09/04/2019
09/04/2019
cho \(\Delta ABC\) có \(\widehat{A}\) =78*. Gọi I là giao điểm của 2 tia phân giác \(\stackrel\frown{B}\) và \(\widehat{C}\)
a) tính \(\widehat{BIC}\)
b) tia phân giác góc ngoài tại \(\widehat{C}\) cắt BI tại E. Tính gói E
Theo dõi (0) 1 Trả lời -


Chứng minh góc EIC=ECI biết tam giác ABC có tia phân giác góc B và C cắt nhau tại I
bởi Nhat nheo
 08/04/2019
08/04/2019
cho tam giác ABC ( AB < AC ) . Tia phân giác của góc B và tia phâ ngiacs của góc C cắt nhau tại I . Qua I kẻ đường thẳng song song với BC cắt AB tại D và cắt AC tại E . Chứng minhh góc DBI bằng góc DIB Chứng minh GÓC EIC = ECI . Các bạn vẽ hình rồi giải giúp mình nhé nhanh lên mình đang cần gấp
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm A, G, H thẳng hàng biết tam giác ABC cân tại A có AB=10cm, BC=12cm
bởi Nguyễn Anh Hưng
 08/04/2019
08/04/2019
Bài 5: Cho tam giác ABC cân tại A, đường cao AH. Biết AB=10cm, BC=12cm.
1. Chứng minh tam giác ABH bằng tam giác ACH
2. Tính độ dài đoạn thẳng AH.
3. Gọi G là trong tâm của tam giác ABC.
a. Chứng minh ba điểm A, G, H thẳng hàng
b. Chứng minh tam giác ABG bằng tam giác ACG
Theo dõi (0) 1 Trả lời -


Tính góc AIC biết tam giác ABC có góc B=60 độ, đường phân giác AP và CQ cắt nhau tại I
bởi thu phương
 08/04/2019
08/04/2019
Cho tam giác ABC có góc B=60o hai đường phân giác AP và CQ của tam giác cắt nhau tại I.
a) Tính góc AIC
b) CM: IP=IQ
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc B = 60 độ. hai tia phân giác AM và CN của tam giác ABN cắt nhau tại I.
a) Tính góc AIC
b) CM : IM = IN
Theo dõi (0) 1 Trả lời -


So sánh KM và KN biết tam giác ABC có các phân giác ngoài góc B và C cắt nhau tại K
bởi hành thư
 09/04/2019
09/04/2019
Cho tam giác ABC các đường phân giác ngoài của góc Bvà góc C cắt nhau ở K.Gọi KM,KN theo thứ tự là các đường vuông góc kẻ từ K đến các đường thẳng AB,AC.
a,So sánh KM và KN
b,Vẽ tia phân giác của góc BAC cắt đường thẳng KC ở E. Chứng minh: AE ⊥ AKTheo dõi (0) 1 Trả lời -


Nêu công thức xác định đường phân giác trong tam giác
Theo dõi (0) 1 Trả lời -


Chứng minh BE=ED=DC biết tam giác ABC cân tại A có phân giác BD và CE cắt tại I
bởi Nguyễn Thanh Hà
 11/04/2019
11/04/2019
Cho tam giác ABC cân tại A. Các đường phân giác BD và CE cắt nhau tại I (D thuộc AC; E thuộc AB). C/minh:
a, BD = CE
b, AI là phân giác của góc A
c, BE = ED = DC
Theo dõi (0) 1 Trả lời -


Chứng minh (AI.BI.CI)/(AM.BN.CP) < = 8/27 biết AM,BN.CP là các phân giác trong
bởi Nguyễn Anh Hưng
 06/11/2018
06/11/2018
Cho tam giác ABC,các đường phân giác trong của tam giác là AM,BN,CP đồng qui tại I. CMR: \(\dfrac{AI.BI.CI}{AM.BN.CP}\)\(\leq\) \(\dfrac{8}{27}\).
Mọi người giúp mình bài này với. Các CTV giúp mình với @Ace Legona,Phương An, Akai Haruma, @Neet
Theo dõi (0) 2 Trả lời






