Giải bài 50 tr 46 sách BT Toán lớp 7 Tập 2
Cho tam giác \(ABC\) có \(\widehat {A} = 70°,\) các đường phân giác \(BD, CE\) cắt nhau ở \(I.\) Tính \(\widehat {BIC}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Tổng ba góc trong tam giác bằng \(180^0.\)
+) Tính chất tia phân giác của một góc.
Lời giải chi tiết
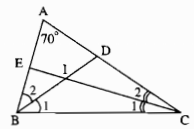
Trong \(∆ABC\) ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
\( \Rightarrow \widehat B + \widehat C = 180^\circ - \widehat A \)\(= 180^\circ - 70^\circ\, = 110^\circ \)
Lại có:
\(\widehat {{B_1}} = \dfrac{1 }{ 2}\widehat B\) (vì \(BD\) là tia phân giác góc \(ABC)\)
\(\widehat {{C_1}} = \dfrac{1 }{2}\widehat C\) (vì \(CE\) là tia phân giác góc \(ACB)\)
Trong \(∆BIC\) ta có:
\(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng 3 góc trong tam giác)
\(\Rightarrow \widehat {BIC} = 180 - (\widehat {{B_1}} + \widehat {{C_1}})\)
\(\widehat {BIC} = 180^\circ - \dfrac{1}{2}(\widehat B + \widehat C) \)\(\,= 180^\circ - \dfrac{1 }{ 2}.110^\circ = 125^\circ \)
-- Mod Toán 7 HỌC247
-


Bài 91 trang 54 SBT Toán 7 tập 2
bởi Nguyễn Anh Hưng
 10/12/2019
Bài 91 (Sách bài tập - tập 2 - trang 54)
10/12/2019
Bài 91 (Sách bài tập - tập 2 - trang 54)Cho tam giác ABC, các đường phân giác của các góc ngoài tại B và C cắt nhau ở E. Gọi G, H, K theo thứ tự là chân các đường vuông góc kẻ từ E đến các đường thẳng BC, Ab, AC
a) Có nhận xét gì về các độ dài EH, EG, EK
b) Chứng minh AE là tia phân giác của góc BAC
c) Đường phân giác của góc ngoài tại A của tam giác ABC cắt các đường thẳng BE, CE tại D, F. Chứng minh rằng EA vuông góc với DF
d) Các đường thẳng AE, BF, CD là các đường gì trong tam giác ABC ?
e) Các đường thẳng EA, FB, DC là các đường gì trong tam giác DEF ?
Theo dõi (0) 1 Trả lời -


Chứng minh hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua 1 điểm
bởi Tram Anh
 11/12/2019
11/12/2019
Cho tam giác ABC .CMR hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua 1 điểm
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm M, E, B thẳng hàng biết tam giác ABC có góc A=90 độ, AB < AC
bởi can tu
 11/12/2019
11/12/2019
Cho tam giác ABC có góc A=90 độ.. AB<AC.Phân giác BE, E thuộc AC. Lấy H thuộc cạnh BC sao cho BH=BA.CM:
a)EH vuông góc BC
b)BE là đường trung trực AH\(\)\(\)
c)Đường thẳng EH cắt AB ở K. CM EK=EC
d)AH//KC
e)Gọi m là trung điểm KC. CM 3 điểm M, E, B thẳng hàng
Theo dõi (0) 1 Trả lời -


Bài 6.4 trang 47 sách bài tập toán 7 tập 2
bởi bala bala
 28/09/2018
Bài 6.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)
28/09/2018
Bài 6.4 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)Hai đườn phân giác \(AA_1\) và \(BB_1\) của tam giác ABC cắt nhau tại M. Hãy tìm các góc ACM, BCM nếu :
a) \(\widehat{AMB}=136^0\)
b) \(\widehat{AMB}=111^0\)
Theo dõi (0) 1 Trả lời -


Bài 6.3 trang 47 sách bài tập toán 7 tập 2
bởi khanh nguyen
 28/09/2018
Bài 6.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)
28/09/2018
Bài 6.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)Cho tam giác ABC. Gọi I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Qua I kẻ đường thẳng song song với BC cắt AB, AC lần lượt tại E và F. Chứng minh EF = BE + CF
Theo dõi (0) 1 Trả lời -


Bài 6.2 trang 47 sách bài tập toán 7 tập 2
bởi Long lanh
 28/09/2018
Bài 6.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)
28/09/2018
Bài 6.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)Cho tam giác ABC có \(\widehat{A}=\widehat{B}+\widehat{C}\). Hai đường phân giác của góc A và góc C cắt nhau tại O. Khi đó góc BOC bằng :
(A) \(85^0\) (B) \(90^0\) (C) \(135^0\) (D) \(150^0\)
Hãy chọn phương án đúng ?
Theo dõi (0) 1 Trả lời -


Bài 6.1 trang 47 sách bài tập toán 7 tập 2
bởi Duy Quang
 28/09/2018
Bài 6.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)
28/09/2018
Bài 6.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 47)Cho tam giác ABC. Trên tia phân giác của góc B, lấy điểm O nằm trong tam giác ABC sao cho O cách đều hai cạnh AB, AC. Khẳng định nào sau đây sai ?
(A) Điểm O nằm trên tia phân giác của góc A
(B) Điểm O không nằm trên tia phân giác của các góc C
(C) Điểm O cách đều AB. BC
(D) Điểm O cách đều AB, AC, BC
Theo dõi (0) 1 Trả lời -


Bài 53* trang 46 sách bài tập toán 7 tập 2
bởi Sam sung
 28/09/2018
Bài 53* (Sách bài tập - tập 2 - trang 46)
28/09/2018
Bài 53* (Sách bài tập - tập 2 - trang 46)Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau ở I. Gọi D và E là chân các đường vuông góc kẻ từ I đến AB và AC
a) Chứng minh rằng AD = AE
b) Tính các độ dài AD, AE biết rằng AB = 6cm, AC = 8cm
Theo dõi (0) 1 Trả lời -


Tính số đo góc BIC biết tam giác ABC có góc A = 70 độ, các đường phân giác BD và CE cắt nhau ở I
bởi Hong Van
 11/12/2019
11/12/2019
cho tam giác ABC có góc A = 70 độ , các đường phân giác BD và CE cắt nhau ở I . tính số đo góc BIC
Theo dõi (0) 1 Trả lời -


Bài 52 trang 46 SBT Toán 7 tập 2
bởi minh thuận
 11/12/2019
Bài 52 (Sách bài tập - tập 2 - trang 46)
11/12/2019
Bài 52 (Sách bài tập - tập 2 - trang 46)Cho tam giác ABC. Các tia phân giác các góc A và C cắt nhau ở I. Các đường phân giác các góc ngoài tại đỉnh A và C cắt nhau ở K. Chứng minh rằng 3 điểm B, I, K thẳng hàng.
Theo dõi (0) 1 Trả lời -


Tính số đo các góc của tam giác DEI biết tam giác ABC có góc B =60 độ
bởi Nguyễn Hồng Tiến
 11/12/2019
11/12/2019
cho tam giác ABC ,góc B =60 độ .Gọi I là giao điểm của hai tia phân giác góc A và góc C .Tia AI cắt BC ở D ,tia CI cắt cạnh AB ở E .Tính số đo các góc của tam giác DEI
Theo dõi (0) 1 Trả lời





