Giải bài 47 tr 47 sách BT Toán lớp 7 Tập 2
Tam giác \(ABC\) có đường trung tuyến \(AM\) đồng thời là đường phân giác. Chứng minh rằng tam giác đó là tam giác cân.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
+) Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
+) Tính chất hai tam giác bằng nhau
+) Tam giác có hay góc kề một cạnh bằng nhau là tam giác cân
Lời giải chi tiết
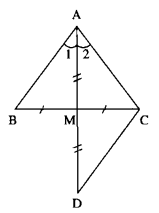
Kẻ \(MH \bot AB,MK \bot {\rm{A}}C\)
AM là tia phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) MH = MK (tính chất tia phân giác)
Xét hai tam giác vuông MHB và MKC:
\(\widehat {MHB} = \widehat {MKC} = 90^\circ \)
MH = MK (chứng minh trên)
MB = MC (gt)
Do đó: ∆MHB = ∆MKC (cạnh huyền, cạnh góc vuông)
\( \Rightarrow \widehat B = \widehat C\)
Vậy ∆ABC cân tại A.
-- Mod Toán 7 HỌC247
-
Chứng minh BD là đường trung trực của CE biết tam giác ABC vuông tại A, E là giao của BA và KD
bởi Nguyen Ngoc
11/04/2019
1. Tam giác ABC vuông tại A , AB = 3cm , AC = 4cm .
a) Tính BC và so sánh các góc của tam giác ABC .
b) Kẻ BD là tia phân giác của góc ABC ( D thuộc AC ) . Kẻ DK vuông góc BC . Chứng minh tam giác ABK cân.
c) Gọi E là giao điểm của BA và KD . Chứng minh BD là đường trung trực của CE .
HELP ME !!!!!!!!!!!!
Theo dõi (0) 1 Trả lời -
Tính số đo góc BIC biết tam giác ABC có góc A=60 độ, 2 tia phân giác góc B và góc C
bởi con cai
11/04/2019
Cho ΔABC có góc A=60độ. Hai tia phân giác của góc B và góc C cắt nhau tại I. Tính số đo góc BIC.
Theo dõi (0) 1 Trả lời -
Tính số đo góc IPH biết góc NMP=70 độ, góc MNP=40 độ
bởi Thanh Truc
12/04/2019
Cho tam giác MNP.Vẽ hai đường phân giác MK và NH cắt nhau tại I.Cho góc NMP bằng 700,góc MNP bằng 400.Hãy tính số đo góc IPH
Theo dõi (0) 1 Trả lời -
So sánh góc DBC và góc DCB biết tam giác ABC cân tại A có D là giao điểm của 3 đường phân giác
bởi thanh hằng
16/04/2019
cho tam giác ABC cân tại A. Gọi D là giao điểm của ba đường phân giác của tam giác đó. Chúng minh am giác ABD = tam giác ACD ; So sánh góc DBC và góc DCB
Theo dõi (0) 1 Trả lời -
Chứng minh MN//BC biết tam giác ABC cân tại A có phân giác góc B cắt AC tại N
bởi Lê Viết Khánh
16/04/2019
cho tam giác ABC cân tại A . Phân giác góc B cắt AC tại N,phân giác góc C cắt AB tại M.
a)c/m : MN//BC
Theo dõi (0) 1 Trả lời -
Tính góc A biết 2 tia phân giác trong của góc B và C cắt nhau tại O và góc BOC=130 độ
bởi Phạm Khánh Ngọc
16/04/2019
Haitia phân giác trong của góc B và góc C của tam giác ABC cắt nhau tại O, biết góc BOC= 130 độ. tính góc A
Theo dõi (0) 1 Trả lời -
Chứng minh DE=BD+CE biết tam giác ABC có phân giác góc B và góc C cắt nhau ở I
bởi Thiên Mai
16/04/2019
cho tam giác ABC, phân giác góc B, góc C cắt nhau ở I. Qua I kẻ đường thẳng BC. Cắt AB ở D, AC ở E
a) CM tam giác BDI cân
b) CM DE=BD+CE
Theo dõi (0) 1 Trả lời -
Tính số đo góc BIC biết tam giác ABC có A=120 độ, BD và CE là 2 phân giác cắt tại I
bởi Choco Choco
25/02/2019
cho tam giác ABC có góc A=120 độ. hai đường phân giác BD và CE cắt nhau tại I
a, tính số đo góc BIC
b, nối AI kéo dài cắt BC tại F. chứng minh DF vuông góc với FE
giúp mk với na các pạn
Theo dõi (0) 1 Trả lời -
Chứng minh D là giao điểm của 3 đường phân giác của tam giác AEF biết tam giác ABC vuông tại A
bởi hồng trang
18/04/2019
Cho tam giác ABC vuông tại A đường phân giác BD qua D kẻ đường thẳng vuông góc với BC tại E cắt BD tại F
Chứng Minh: D là giao điểm của 3 đường phân giác của tam giác AEF
Theo dõi (0) 1 Trả lời -
Bài 3: Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC (H thuộc BC).Gọi M là trung điểm của BH.Trên tia đối của tia MA lấy điểm N sao cho MN = MA
a) CMR: tam giác AMH = tam giác NMB và NB vuông góc với BC
b) CMR: AH = NB,từ đó suy ra NB < AB
c) Gọi K là trung điểm của NC. Chứng minh ba điểm A,H,K thẳng hàng
Theo dõi (0) 1 Trả lời -
Chứng minh 3 điểm O, M, H thẳng hàng biết góc xOy=60 độ, trên tia phân giác góc xOy lấy điểm H
bởi Trần Phương Khanh
18/04/2019
Cho góc xOy=60, trên tia phân giác của góc xOy lấy điểm H. Từ M kẻ MA vuông góc với Ox( A thuộc Ox), kẻ MB vuông góc với Oy( B thuộc Oy).
a, Chứng minh rằng OA=OB và tam giác OAB đều.
b, Gọi E là giao điểm của BM và Ox, F là giao điểm của AM và Oy. Chứng minh rằng tam giác BMF=Tam giác AME.
c, Gọi H là trung điểm của FE. Chứng minh 3 điểm O, M, H thẳng hàng.
Theo dõi (0) 1 Trả lời
