Giải bài 28 tr 141 sách BT Toán lớp 7 Tập 1
Cho hai tam giác \(ABC\) và \(ABD\) có \(AB = BC = CA = 3cm\), \(AD = BD = 2cm\) (\(C\) và \(D\) nằm khác phía đối với \(AB\)). Chứng minh rằng: \(\widehat {CA{\rm{D}}} = \widehat {CB{\rm{D}}}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
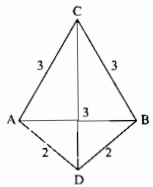
Xét ∆ CAD và ∆ CBD ta có:
AC = BC (gt)
AD = BD (gt)
CD cạnh chung
Suy ra: ∆CAD = ∆CBD (c.c.c)
Vậy \(\widehat {CA{\rm{D}}} = \widehat {CB{\rm{D}}}\) (hai góc tương ứng)
-- Mod Toán 7 HỌC247
-


Cho tam giác ABC biết AB= BC . M là trung điểm của cạnh BC
A) Chứng minh góc BAM = góc CAM
B) Chứng minh AM vuông góc với BC
Theo dõi (0) 1 Trả lời -


Chứng minh AB//CD, AD//BC biết AB=DC, AD=BC
bởi Nguyễn Hồng Tiến
 09/04/2019
09/04/2019
cho hình vẽ: chứng minh: AB //CD
AD //BC
AI LÀM NHANH NHẤT MK TICK CHO
 HIHIHI...........Theo dõi (0) 1 Trả lời
HIHIHI...........Theo dõi (0) 1 Trả lời -


Cho \(\widehat{xOy}\) nhọn, trên tia Ox, Oy lấy tương ứng 1 điểm A và B sao cho OA = OB. Vẽ đường tròn tâm A và đường tròn tâm B có cùng bán kính sao cho chúng cắt nhau tại M và N nằm trong \(\widehat{xOy}\). CM
a) Δ OMA = Δ OMB và Δ ONA = Δ ONB
b) 3 điểm O, M, N thẳng hàng
c) Δ AMN = Δ BMN
d) MN là tia p/g \(\widehat{AMB}\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABM=ACM biết tam giác ABC vuông cân tại A, M là trung điểm BC
bởi can chu
 09/04/2019
09/04/2019
Cho △ ABC vuông cân tại A, M là trung điểm của BC. E nằm giwuax M và C. Kẻ bh và CD ⊥ AE
a, CM △ ABM = △ACM
b, CM \(\widehat{CAD}\) = \(\widehat{ABH}\) và BH = CD
c, △MHD là △cân
Vẽ hình như sau :
Các man cứ việc giải hộ nha @@@ Mơn :)))
Theo dõi (0) 1 Trả lời -


Chứng minh AD vuông góc với BC biết tam giác ABC vuông tại A có I là trung điểm BC
bởi Co Nan
 09/04/2019
09/04/2019
cho tam giác ABC vuông tại A, có I là trung điểm của BC. Trên tia đối của tia IA lấy điểm D sao cho IA=ID và AB=AC, chứng minh rằng AD vuông góc với BC
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có góc A= 100 độ ;AB=AC.N là một điểm nằm trong tam giác sao cho NB=NC.Khi đó góc BAN=?
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABM=ACM biết tam giác ABC có cạnh AB=AC, M là trung điểm của BC
bởi Mai Thuy
 09/04/2019
09/04/2019
Cho tam giác ABC có cạnh AB=AC,M là trung điểm của BC
a. chứng minh △ABM=△ACM
b. trên tia đối của tia MA lấy điểm D sao cho MD=MA. Chứng minh AC=BD
c. chứng minh AB song song với CD
d. trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia Ax song song với BC lấy điểm I ϵ Ax sao cho AI=BC. Chứng minh 3 điểm D,C,I thẳng hàng.
Theo dõi (0) 1 Trả lời -


Chứng minh AM vuông góc với BC biết tam giác ABC có AB=AC, M là trung điểm BC
bởi Nguyễn Trà Giang
 22/02/2019
22/02/2019
Cho tam giác ABC , AB=AC , M là trung điểm BC
a. Tam giác ABM =tam giác ACM
b. AM là p/g góc BAC
c. AM vuông góc với BC
d. Trên nửa mp BC ko chứa A lấy D sao cho DB=DC.cm A,M,D thẳng hàng
Theo dõi (0) 1 Trả lời -


Tính góc B, góc C biết AB=AD, BC=CD và góc BAC=30 độ
bởi Suong dem
 22/02/2019
Theo dõi (0) 1 Trả lời
22/02/2019
Theo dõi (0) 1 Trả lời -


Chứng minh BD song song AM biết từ A kẻ AD song song với BM sao cho AD=BM
bởi Nguyễn Thị Trang
 09/04/2019
09/04/2019
Cho tam giác ABC , M là trung điểm của BC, I là trung điểm của AB. Từ A kẻ AD song song BM / AD = BM, B và M nằm khác phía so với AD.
a) Chứng minh tam giác DAB = tam giác MBA
b) Chứng minh DI = IM ; M I D thẳng hàng
c) Chứng minh BD song song AM
GIÚP MỊ VỚI MỊ CẦN GẤP LẮM LUÔN Ý !!!
 GIÚP MỊ NHA !!! TKS NHÌU
GIÚP MỊ NHA !!! TKS NHÌU  Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh OM là tia phân giác góc xOy biết OC=OA , OB=OD và M là giao điểm của AD và BC
bởi Lê Chí Thiện
 09/04/2019
09/04/2019
Bài 1,Cho tam giác ABC qua A kẻ đường thẳng song song với BC , qua C kẻ đường thẳng song song với AB hai đường thẳng này cắt nhau tại D
a, chứng minh tam giác ABC bằng tam giác ADC
b, Chứng minh hai tam giác ADB và ADC bằng nhau
c, Gọi O là giao điểm của AC và BD
Chứng minh hai tam giác ABO và COD bằng nhauBài 2, Cho góc xOy khác góc bẹt . Lấy các điểm A,B thuộc tia Ox sao cho OA bé hơn OB. Lấy các điểm C,D thuộc tia Oy sao cho OC = OA , OB = OD Gọi M là giao điểm của AD và BC . Chứng minh rằng
a, AD = BC
b, tam giác MAB = tam giác MCD
c,OM là tia phân giác của góc xOyTheo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 23 trang 115 SGK Toán 7 Tập 1
Bài tập 27 trang 140 SBT Toán 7 Tập 1
Bài tập 29 trang 141 SBT Toán 7 Tập 1
Bài tập 30 trang 141 SBT Toán 7 Tập 1
Bài tập 31 trang 141 SBT Toán 7 Tập 1
Bài tập 32 trang 141 SBT Toán 7 Tập 1
Bài tập 33 trang 141 SBT Toán 7 Tập 1
Bài tập 34 trang 141 SBT Toán 7 Tập 1
Bài tập 35 trang 141 SBT Toán 7 Tập 1
Bài tập 3.1 trang 141 SBT Toán 7 Tập 1





