Phần hướng dẫn giải bài tập SGK Hình học 7 Chương 2 Bài 3 Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (ccc) sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 7 Tập một
-
Bài tập 15 trang 114 SGK Toán 7 Tập 1
Vẽ tam giác MNP, biết MN=2,5 cm, NP=3cm, PM= 5cm.
-
Bài tập 16 trang 114 SGK Toán 7 Tập 1
Vẽ tam giác biết độ dài mỗi cạnh là 3 cm. Sau đó đo góc của mỗi tam giác.
-
Bài tập 17 trang 114 SGK Toán 7 Tập 1
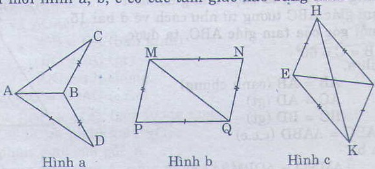
Trên mỗi hình sau có tam giác nào bằng nhau? Vì sao?
-
Bài tập 18 trang 114 SGK Toán 7 Tập 1
Xét bài toán: "
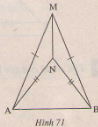
AMB và
ANB có MA=MB, NA=NB(h.71). Chứng minh rằng
\(\widehat{AMN}=\widehat{BMN}\)."
1) Hãy ghi giả thiết và kết luận của bài toán.
2) Hãy sắp xếp bốn câu sau đây một cách hợp lý để giải bài toán trên :
a) Do đó
AMN=
BMN(c.c.c)
b) MN: cạnh chung
MA=MB( Giả thiết)
NA= NB( Giả thiết)
c) Suy ra
(2 góc tương ứng)
d)
AMB và
ANB có:
-
Bài tập 19 trang 114 SGK Toán 7 Tập 1
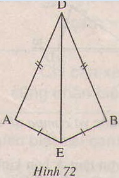
Cho hình 72. Chứng minh rằng:
a) ∆ADE = ∆BDE.
b) \(\widehat{DAE}=\widehat{DBE}\).
-
Bài tập 20 trang 114 SGK Toán 7 Tập 1
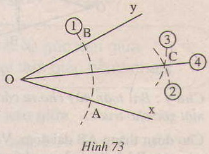
Cho góc xOy(h.73), Vẽ cung tròn tâm O, cung tròn này cắt Ox, Oy theo thứ tự ở A,B (1). Vẽ các cung tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong góc xOy ((2) (3)). Nối O với C (4). Chứng minh OC là tia phân giác của góc xOy.
-
Bài tập 21 trang 115 SGK Toán 7 Tập 1
Cho tam giác ABC, Dùng thước và compa, vẽ các tia phân giác của các góc A,B,C.
-
Bài tập 22 trang 115 SGK Toán 7 Tập 1
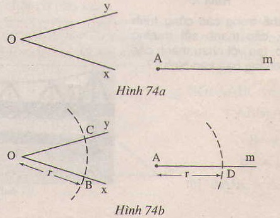
Cho góc xOy và tia Am(h.74a)
Vẽ cung trong tâm O bán kính r, Cung tròn này cắt Ox,Oy theo thứ tự ở B,C
Vẽ cung tròn tâm A bán kính R, cung này cắt kia Am ở D(h.74b).
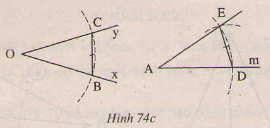
Vẽ cung tròn tâm D có bán kính bằng BC, cung tròn này cắt cung tròn tam A bán kính r ở E(h. 74c).
Chứng minh rằng
-
Bài tập 23 trang 115 SGK Toán 7 Tập 1
Cho đoạn thẳng AB dài 4cm Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 3cm, chúng cắt nhau ở C và D, chứng minh rằng AB là tia phân giác của góc CAD.
-
Bài tập 27 trang 140 SBT Toán 7 Tập 1
Vẽ tam giác \(ABC\) biết độ dài mỗi cạnh bằng \(2,5cm\). Sau đó đo mỗi góc của tam giác.
-
Bài tập 28 trang 141 SBT Toán 7 Tập 1
Cho hai tam giác \(ABC\) và \(ABD\) có \(AB = BC = CA = 3cm\), \(AD = BD = 2cm\) (\(C\) và \(D\) nằm khác phía đối với \(AB\)). Chứng minh rằng: \(\widehat {CA{\rm{D}}} = \widehat {CB{\rm{D}}}\).
-
Bài tập 29 trang 141 SBT Toán 7 Tập 1
Cho góc \(xOy.\) Trên tia \(Ox\) lấy điểm \(C\), trên tia \(Oy\) lấy điểm \(D\) sao cho \(OD = OC.\) Vẽ các cung tròn tâm \(C\) và tâm \(D\) có cùng bán kính sao cho chúng cắt nhau ở điểm \(E\) nằm trong góc \(xOy.\) Chứng minh rằng \(OE\) là tia phân giác của góc \(xOy\).
-
Bài tập 30 trang 141 SBT Toán 7 Tập 1
Tìm chỗ sai trong bài làm sau đây của một học sinh (hình dưới).
∆ABC = ∆DCB (c.c.c)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}}\) (cặp góc tương ứng)
\( \Rightarrow \) BC là tia phân giác của góc ABD

-
Bài tập 31 trang 141 SBT Toán 7 Tập 1
Vẽ tam giác \(ABC\) có \(AB = AC = 6cm, BC = 2cm.\) Sau đó đo góc \(A\) để kiểm tra rằng \(\widehat A \approx 20^\circ \).
-
Bài tập 32 trang 141 SBT Toán 7 Tập 1
Tam giác \(ABC\) có \(AB = AC\), \(M\) là trung điểm của \(BC.\) Chứng minh rằng \(AM\) vuông góc với \(BC.\)
-
Bài tập 33 trang 141 SBT Toán 7 Tập 1
Cho đoạn thẳng \(AB.\) Vẽ cung tròn tâm \(A\) bán kính \(AB\) và cung tròn tâm \(B\) bán kính \(BA\), chúng cắt nhau ở \(C\) và \(D.\) Chứng minh rằng:
a) \(∆ABC = ∆ABD\).
b) \(∆ACD = ∆BCD\).
-
Bài tập 34 trang 141 SBT Toán 7 Tập 1
Cho tam giác \(ABC.\) Vẽ cung tròn tâm \(A\) bán kính bằng \(BC\), vẽ cung tròn tâm \(C\) bán kính bằng \( BA\), chúng cắt nhau ở \(D\) (\(D\) và \(B\) nằm khác phía đối với \(AC\)). Chứng minh rằng \(AD // BC.\)
-
Bài tập 35 trang 141 SBT Toán 7 Tập 1
Cho đường thẳng \(xy\), các điểm \(B\) và \(C\) nằm trên \(xy\), điểm \(A\) nằm ngoài \(xy.\) Dựa vào bài \(34\), hãy nêu cách vẽ đường thẳng đi qua \(A\) và song song với \(BC.\)
-
Bài tập 3.1 trang 141 SBT Toán 7 Tập 1
Cho hình bs 1. Điền vào chỗ trống:
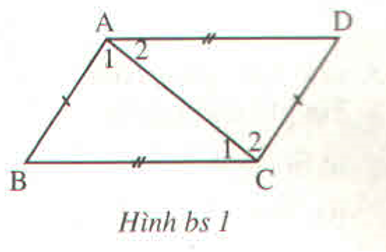
\(\begin{array}{l}
\widehat {{A_1}} = ...\\
\widehat {{A_2}} = ...\\
\widehat B = ...
\end{array}\) -
Bài tập 3.2 trang 142 SBT Toán 7 Tập 1
a) Vẽ tam giác \(ABC\) có \(BC = 2cm, AB = AC = 3cm.\)
b) Gọi \(E\) là trung điểm của cạnh \(BC\) của tam giác \(ABC\) trong câu a). Chứng minh rằng \(AE\) là tia phân giác của \(BAC.\)
-
Bài tập 3.3 trang 142 SBT Toán 7 Tập 1
Cho bốn điểm \(A, B, C, D\) thuộc đường tròn \((O)\) sao cho \(AB = CD.\) Chứng minh rằng \(\widehat {AOB} = \widehat {COD}\).






