Toán 10 Bài 2: Tập hợp

Lý thuyết10 Trắc nghiệm29 BT SGK 81 FAQ

Tập hợp là một khái niệm các em đã được tìm hiểu ở chương trình Toán 6. Chương trình Đại số 10, tiếp tục kế thừa và giới thiệu đến các em thêm những khái niệm, dạng bài tập mới. Xin mời các em cùng tìm hiểu nội dung bài học.

YOMEDIA

1. Tóm tắt lý thuyết

1.1. Tập hợp

1.2. Cách xác định tập hợp

1.3. Tập con

1.4. Tập hợp bằng nhau

2. Bài tập minh hoạ

3. Luyện tập bài 2 chương 1 đại số 10

3.1. Trắc nghiệm tập hợp

3.2. Bài tập SGK & Nâng cao tập hợp

4. Hỏi đáp về bài 2 chương 1 đại số 10

Tóm tắt lý thuyết

1.1. Tập hợp

Tập hợp là khái niệm cơ bản của toán học, không định nghĩa .
Tập hợp thường được kí hiệu bằng các chữ cái in hoa như: A, B, C, D, .... các phần tử của tập hợp đặt trong cặp dấu { }.
Để chỉ phần tử a thuộc tập hợp A ta viết \(a \in A,\) ngược lại ta viết \(a \notin A.\)
Tập hợp không chứa phần tử nào gọi là tập rỗng. Khí hiệu \(\emptyset .\)

1.2. Cách xác định tập hợp

Có 2 cách:

Cách 1: Liệt kê các phần tử : mỗi phần tử liệt kê một lần, giữa các phần tử có dấu phẩy hoặc dấu chấm phẩy ngăn cách. Nếu số lượng phần tử nhiều có thể dùng dấu ba chấm.

Ví dụ:

A = {1; 3; 5; 7}

B = {0 ; 1; 2; . . . . ; 100 }

C= {1; 3; 5;…;15; 17}

Cách 2: Chỉ rõ tính chất đặc trưng của các phần tử trong tập hợp, tính chất này được viết sau dấu gạch đứng.

Ví dụ:

A = {\(x \in \mathbb{N}\) | x lẻ và x <9}; B= {\(x \in \mathbb{R}\)| 2x²-5x+3=0}

1.3. Tập con

Nếu tập A là con của B, kí hiệu: \(A \subset B\) hoặc \(B \supset A.\) .
Khi đó \(A \subset B \Leftrightarrow \forall x\left( {x \in A \Rightarrow x \in B} \right)\)

Ví dụ:

A={1;3;5;7;9}, B={1;2;3;...;10}

Cho \(A \ne \emptyset \) có ít nhất 2 tập con là \(\emptyset \) và A.

Tính chất:

\(A \subset A,\emptyset \subset A\) với mọi A.

Nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)

1.4. Tập hợp bằng nhau

\(A = B \Leftrightarrow A \subset B\) và \(B \subset A\) hay \(A = B \Leftrightarrow \forall x\left( {x \in A \Leftrightarrow x \in B} \right)\)

Ví dụ:

\(\begin{array}{l}C = \left\{ {x \in \mathbb{R}|2{x^2} - 5x + 2 = 0} \right\}\\D = \left\{ {\frac{1}{2};1} \right\}\\ \Rightarrow C = D.\end{array}\)

Biểu đồ Ven

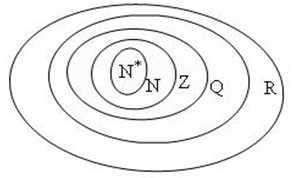
Biểu đồ Ven các tập số

Ta có \(\mathbb{N}* \subset \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)

Bài tập minh họa

Ví dụ 1:

Cho các tập hợp sau:

a) Tập hợp A là các nghiệm của phương trình \((x + 1)(x + 3)\left( {x - \frac{1}{2}} \right) = 0.\)

b) Tập \(B = \left\{ {m \in \mathbb{Z}|{m^2} \le 50} \right\}\)

Hãy liệt kê tất cả các phần tử của chúng.

Hướng dẫn giải:

a) \(A = \left\{ { - 3; - 1;\frac{1}{2}} \right\}\)

b) \(B = \left\{ { - 7; - 6; - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5;6;7} \right\}.\)

Ví dụ 2:

Tìm tất cả các tập hợp con của tập hợp \(A = \left\{ { - 3;0;2} \right\}.\)

Hướng dẫn giải:

Tập A có 8 tập hợp con là: \(\emptyset ,\left\{ { - 3} \right\},\left\{ 0 \right\},\left\{ 2 \right\},\left\{ { - 3;0} \right\},\left\{ { - 3;2} \right\},\left\{ {0;2} \right\},\left\{ { - 3;0;2} \right\}.\)

Ví dụ 3:

Tìm các tính chất đặc trưng của các tập hợp sau:

a) \(A = \left\{ {1;\frac{1}{2};\frac{1}{3};\frac{1}{4};\frac{1}{5};\frac{1}{6}} \right\}\)

b) \(B = \left\{ {\frac{5}{4};\frac{{10}}{9};\frac{{17}}{{16}};\frac{{26}}{{25}};\frac{{37}}{{36}};\frac{{50}}{{49}}} \right\}.\)

Hướng dẫn giải:

a) \(A = \left\{ {\frac{1}{n}|n \in \mathbb{N},1 \le n \le 6} \right\}.\)

b) \(B = \left\{ {\frac{{{n^2} + 1}}{{{n^2}}}|n \in \mathbb{N},2 \le n \le 7} \right\}.\)

3. Luyện tập Bài 2 chương 1 đại số 10

Trong phạm vi bài học HỌC247 chỉ giới thiệu đến các em những nội dung cơ bản nhất về khái niệm cơ bản nhất của mệnh đề. Về các thuật ngữ có vẻ hết sức quen thuộc. Khái niệm Tập hợp các em đã bước đầu được tìm hiểu ở chương trình Toán lớp 6, lên bậc THPT chúng ta sẽ được học nâng cao hơn, các em cần tìm hiểu thêm.

3.1 Trắc nghiệm về tập hợp

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Chương 1 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Hãy liệt kê các phần tử của tập hợp: \(X = \left\{ {x \in \mathbb{R}|{x^2} + x + 1 = 0} \right\}\)
- A. \(X = 0\)
- B. \(X = \left\{ 0 \right\}\)
- C. \(X = \emptyset \)
- D. \(X = \left\{ \emptyset \right\}\)
Câu 2:
Trong các mệnh đề sau, tìm mệnh đề sai?
- A. \(A \in A\)
- B. \(\emptyset \subset A\)
- C. \(A \subset A\)
- D. \(A \in \left\{ A \right\}\)
Câu 3:
Cho tập hợp \(A = \left\{ {1;2;\left\{ {3;4} \right\};x;y} \right\}.\)

Xét các mệnh đề dưới đây:

\(\begin{array}{l}(I):3 \in A\\(II):\left\{ {3;4} \right\} \in A\\(III):\left\{ {a;3;b} \right\} \notin A\end{array}\)

Chọn phương án đúng?
- A. Chỉ I đúng.
- B. I, II đúng.
- C. II, III đúng.
- D. Cả I, II, III đều đúng.

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK và Nâng Cao về tập hợp

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Chương 1 Bài 2 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Đại số 10 Cơ bản và Nâng cao.

Bài tập 1 trang 13 SGK Đại số 10

Bài tập 2 trang 13 SGK Đại số 10

Bài tập 3 trang 13 SGK Đại số 10

Bài tập 1.19 trang 11 SBT Toán 10

Bài tập 1.20 trang 11 SBT Toán 10

Bài tập 1.21 trang 11 SBT Toán 10

Bài tập 1.22 trang 11 SBT Toán 10

Bài tập 1.23 trang 12 SBT Toán 10

Bài tập 22 trang 20 SGK Toán 10 NC

Bài tập 23 trang 20 SGK Toán 10 NC

Bài tập 24 trang 21 SGK Toán 10 NC

Bài tập 25 trang 21 SGK Toán 10 NC