Giải bài 62 tr 91 sách GK Toán 9 Tập 2
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ đường tròn (O;R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ đường tròn (O;r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O;R).
Hướng dẫn giải chi tiết bài 62
Để vẽ được hình như bài 62, chúng ta chỉ cần thước và compa là có thể giải quyết được bài toán.
.png)
Câu a:
Vẽ tam giác đều ABC có cạnh bằng 3cm bằng cách vẽ đoạn AB bằng 3cm, sau đó, vẽ hai cung tròn tâm A và tâm B cũng có bán kính bằng 3cm.
Giao hai cung tròn đó là điểm C. Ta được tam giác ABC
Câu b:
Gọi H là chân đường vuông góc của O đến BC (hình vẽ)
Vì ABC là tam giác đều, nên tâm đường tròn ngoại tiếp và nội tiếp của tam giác này là trùng nhau.
Xét tam giác BOH vuông tại H có:
\(\small BH=\frac{1}{2}BC=1,5(cm)\)
\(\small \widehat{OBH}=30^o\)
\(\small \Rightarrow R=OB=\sqrt{3}(cm)\)
Câu c:
OH cũng là tâm của đường tròn nội tiếp tam giác ABC
Vậy ta vẽ đường tròn tâm O, bán kính OH
Theo câu trên, ta sẽ tính được bán kính đường tròn nội tiếp tam giác ABC:
\(\small r=OH=\frac{\sqrt{3}}{2}(cm)\)
Câu d:
Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K
Ta có tam giác IJK là tam giác đều ngoại tiếp (O;R) thỏa yêu cầu bài toán!
-- Mod Toán 9 HỌC247
-


Diện tích hình vuông là 16cm^2. Tính diện tích hình tròn nội tiếp hình vuông
bởi Ngại Va Chạm
 26/05/2020
Hộ em với cảm ơn ạTheo dõi (0) 0 Trả lời
26/05/2020
Hộ em với cảm ơn ạTheo dõi (0) 0 Trả lời -


Vẽ đường tròn đi qua 3 đỉnh của hình thang, hình bình hành, hình thoi Vẽ đường tròn đi qua 3 đỉnh của hình chữ nhật, hình vuông, hình thang cân
bởi Quynh Anh Nguyen
 20/05/2020
Theo dõi (0) 0 Trả lời
20/05/2020
Theo dõi (0) 0 Trả lời -


Vẽ đường tròn đi qua 3 đỉnh của hình thang, hình bình hành, hình thoi
bởi Quynh Anh Nguyen
 20/05/2020
Đường tròn nội tiếp Đường tròn ngoại tiếpTheo dõi (0) 0 Trả lời
20/05/2020
Đường tròn nội tiếp Đường tròn ngoại tiếpTheo dõi (0) 0 Trả lời -


Chứng minh tứ giác ABMD nội tiếp?
bởi Nguyên Tung
 13/05/2020
13/05/2020
⁹
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh tam giác FME cân?
bởi Kim Khánh
 08/05/2020
08/05/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho tam giác ABC có góc ABC=120 độ ,AB=12cm và nội tiếp đường tròn tâm O. Khi đó bán kính nội tiếp đường tròn tâm O là?
bởi Linh Thuỳ
 22/04/2020
Theo dõi (0) 0 Trả lời
22/04/2020
Theo dõi (0) 0 Trả lời -


Tính bán kính R,r của đường tròn ngoại tiếp, nội tiếp đa giác đó theo a và n?
bởi Ngọc Nhàn Ngọc Nhàn
 10/04/2020
10/04/2020
Bài 2
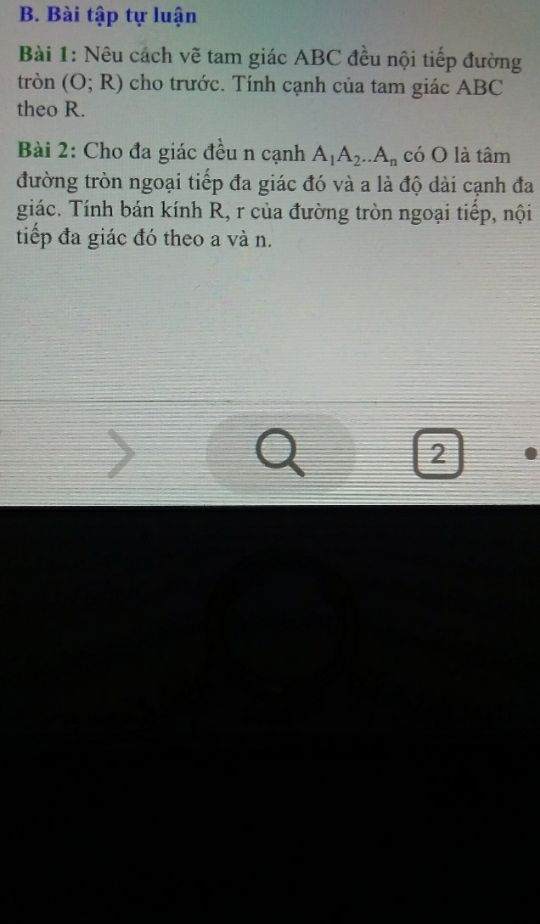 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Viết phương trình đường thẳng (d) đi qua B(0;1) và có hệ số góc k và chứng tỏ (d) luôn cắt parabol (P): y=x^2 tại 2 điểm phân biệt
bởi Lê Khả Hải
 14/03/2020
14/03/2020
Giải bài 3
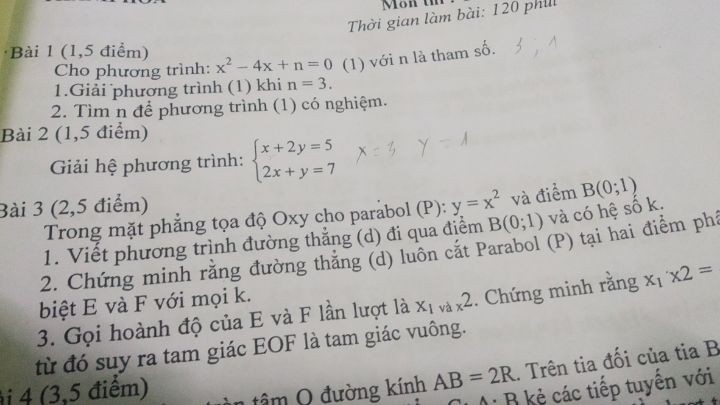 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho 3 đường tròn (A;R1),(B;R2)và (C;R3) đôi một tiếp xúc với nhau tính r1 r2 r3 biết AB=5, AC=6,BC=7
bởi V H
 23/11/2019
23/11/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh NE vuông góc với AB
bởi Nguyễn Lê Thảo Trang
 28/12/2018
28/12/2018
Cho đường tròn tâm O , đường kính AB , vẽ điểm N đối xứng A qua M , BN cắt đường điểm C , E là giao của AC và BM .
a) Chứng minh : NE vuông góc với AB .
b) Gọi F đối xứng với E qua M . Chứng minh ; FA là tiếp tuyến của đường tròn tâm O
c) FN là tiếp tuyến đường tròn tâm O , bán kính BA
Theo dõi (0) 1 Trả lời -


Chứng minh CF là tia phân giác của góc DCN
bởi bala bala
 02/01/2019
02/01/2019
Cho nửa đường tròn tâm O, đường kính AB. Lấy điểm C trên OB \(\left(C\ne O;C\ne B\right)\) sao cho đường thẳng (d) đi qua C vuông góc với AB. Đường thẳng (d) cắt nửa đường tròn (O) tại M, lấy điểm \(N\in\stackrel\frown{MB}\) , tia AN cắt (d) tại F, tia BN cắt (d) tại E. Biết AE cắt nửa đường tròn (O) tại D, chứng minh rằng: \(CF\) là tia phân giác của góc \(DCN\).
Theo dõi (0) 1 Trả lời -


Tính bán kính biết AB=8cm, AC=15cm, AH=5cm
bởi Bánh Mì
 03/01/2019
03/01/2019
Cho tam giác ABC nội tiếp trong (O) với đường cao AH ( H thuộc BC )
a) Tính bán kính ( O ) biết AB=8cm , AC=15cm , AH=5cm
Theo dõi (0) 1 Trả lời -


Gọi I là trung điểm của CD, chứng minh bốn điểm A,B,O,I nằm trên một đường tròn
bởi bich thu
 02/01/2019
02/01/2019
Cho đường tròn tâm O và M là điểm ở ngoài đường tròn. Qua M kẻ tiếp tuyến MA, MB (A, B là tiếp điểm) và một cát tuyến cắt đường tròn tại C, D,
a/ Gọi I là trung điểm của CD. Chứng minh bốn điểm A,B,O,I nằm trên một đường tròn.
b/ AB cắt CD tại E. Chứng minh MA^2=ME.MI
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 61 trang 91 SGK Toán 9 Tập 2
Bài tập 63 trang 92 SGK Toán 9 Tập 2
Bài tập 64 trang 92 SGK Toán 9 Tập 2
Bài tập 44 trang 107 SBT Toán 9 Tập 2
Bài tập 45 trang 107 SBT Toán 9 Tập 2
Bài tập 46 trang 107 SBT Toán 9 Tập 2
Bài tập 47 trang 108 SBT Toán 9 Tập 2
Bài tập 48 trang 108 SBT Toán 9 Tập 2
Bài tập 49 trang 108 SBT Toán 9 Tập 2
Bài tập 50 trang 108 SBT Toán 9 Tập 2
Bài tập 51 trang 108 SBT Toán 9 Tập 2





