Bài tập 49 tr 108 sách BT Toán lớp 9 Tập 2
Tính cạnh của hình tám cạnh đều theo bán kính \(R\) của đường tròn ngoại tiếp.
Hướng dẫn:
Cách \(1:\) áp dụng công thức \(a = 2R\sin\displaystyle {{180^\circ } \over n}\)
Cách \(2:\) tính trực tiếp.
Vẽ dây \(AB\) là cạnh của một hình vuông nội tiếp đường tròn \((O),\) gọi \(C\) là điểm chính giữa của cung nhỏ \(AB.\) Khi đó \(CA\) là cạnh của hình tám cạnh đều nội tiếp. Hãy tính \(CA\) trong tam giác vuông \(CAC’.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
+) Trong tam giác vuông, bình phương cạnh góc vuông bằng tích cạnh huyền với hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Lời giải chi tiết
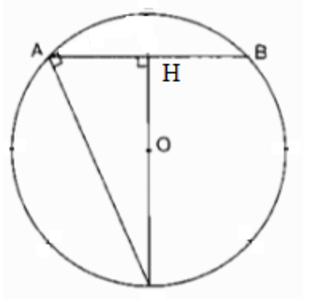
AB là cạnh của đa giác đều 8 cạnh.
Kẻ OH ⊥ AB \( \Rightarrow \) HA =HB \( = {1 \over 2}AB\)
\( \Rightarrow \widehat {HOB} = {{180^\circ } \over 8} = 22^\circ 30'\)
Trong tam giác vuông HOB ta có:
HB = OB. sin\(\widehat {HOB}\) \( \Rightarrow AB = 2.OB.\sin \widehat {HOB} = 2.R.\sin 22^\circ 30' \approx 0,764R\)
-- Mod Toán 9 HỌC247
-


Bài 84 trang 171 sách bài tập Toán 9 tập 1
bởi Mai Rừng
 04/01/2019
Bài 84 (Sách bài tập trang 171)
04/01/2019
Bài 84 (Sách bài tập trang 171)Cho tam giác ABC vuông tại A( AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng :
a) Tam giác EBF là tam giác cân
b) Tam giác HAF là tam giác cân
c) HA là tiếp tuyến của đường tròn (O)
Theo dõi (0) 1 Trả lời -


Bài 83 trang 171 sách bài tập Toán 9 tập 1
bởi Thụy Mây
 04/01/2019
Bài 83* (Sách bài tập trang 171)
04/01/2019
Bài 83* (Sách bài tập trang 171)Cho hai đường tròn (O) và (O') cắt nhau tại A và B, OO' = 3cm. Qua A kẻ một đường thẳng cắt các đường tròn (O) và (O') theo thứ tự tại E và F (A nằm giữa E và F). Tính xem đoạn thẳng EF có độ dài lớn nhất bằng bao nhiêu ?
Theo dõi (0) 1 Trả lời -


Bài 82 trang 171 sách bài tập Toán 9 tập 1
bởi Anh Trần
 04/01/2019
Bài 82 (Sách bài tập trang 171)
04/01/2019
Bài 82 (Sách bài tập trang 171)Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài DE, \(D\in\left(O\right),E\in\left(O'\right)\). Kẻ tiếp tuyến chung trong tại A, cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O'I và AE
a) Tứ giác AMIN là hình gì ? Vì sao ?
b) Chứng minh hệ thức IM.IO = IN.IO'
c) Chứng minh rằng OO' là tiếp tuyến của đường tròn có đường kính là DE
d) Tính độ dài DE biết rằng OA = 5cm, O'A = 3,2cm
Theo dõi (0) 1 Trả lời -


Bài 81 trang 171 sách bài tập Toán 9 tập 1
bởi Vũ Hải Yến
 04/01/2019
Bài 81 (Sách bài tập trang 171)
04/01/2019
Bài 81 (Sách bài tập trang 171)Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N
a) Tứ giác DMCN là hình gì ? Vì sao ?
b) Chứng minh hệ thức DM.DA = DN.DB
c) Chứng minh MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB
d*) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất ?
Theo dõi (0) 1 Trả lời -


Bài 80 trang 170 sách bài tập Toán 9 tập 1
bởi Mai Bảo Khánh
 04/01/2019
Bài 80 (Sách bài tập trang 170)
04/01/2019
Bài 80 (Sách bài tập trang 170)Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O';1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O) ?
Theo dõi (0) 1 Trả lời -


Bài 79 trang 170 sách bài tập Toán 9 tập 1
bởi Hy Vũ
 04/01/2019
Bài 79 (Sách bài tập trang 170)
04/01/2019
Bài 79 (Sách bài tập trang 170)Cho đường tròn (O; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A; 2R)
a) Hai đường tròn (O) và (A) có vị trí tương đối như thế nào đối với nhau ?
b) Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm (khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC ?
Theo dõi (0) 1 Trả lời -


Bài 78 trang 170 sách bài tập Toán 9 tập 1
bởi Spider man
 04/01/2019
Bài 78 (Sách bài tập trang 170)
04/01/2019
Bài 78 (Sách bài tập trang 170)Cho hai đường tròn (O; 2cm) và (O'; 3cm). OO' = 6cm
a) Hai đường tròn (O), (O') có vị trí tương đối như thế nào đối với nhau ?
b) Vẽ đường tròn (O'; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O'A cắt đường tròn (O';3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O'B, B và C thuộc cùng một nửa mặt phẳng có bờ OO'. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm) và (O'; 3cm)
c) Tính độ dài BC
d) Gọi I là giao điểm của BC và OO'. Tính độ dài IO ?
Theo dõi (0) 1 Trả lời -


Bài 77* trang 169 sách bài tập Toán 9 tập 1
bởi Lê Văn Duyệt
 04/01/2019
Bài 77* (Sách bài tập trang 169)
04/01/2019
Bài 77* (Sách bài tập trang 169)Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN với M thuộc (O) và N thuộc (O'). Gọi P là điểm đối xứng với M qua OO', Q là điểm đối xứng với N qua OO'. Chứng minh rằng :
a) MNQP là hình thang cân
b) PQ là tiếp tuyến chung cả hai đường tròn (O) và (O')
c) MN + PQ = MP + NQ
Theo dõi (0) 1 Trả lời -


Bài 76 trang 169 sách bài tập Toán 9 tập 1
bởi na na
 04/01/2019
Bài 76 (Sách bài tập trang 169)
04/01/2019
Bài 76 (Sách bài tập trang 169)Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO'C. Gọi DE là tiếp tuyến chung của hai đường tròn. \(D\in\left(O\right),E\in\left(O'\right)\). Gọi M là giao điểm của BD và CE
a) Tính số đo góc DAE
b) Tứ giác ADME là hình gì ? Vì sao ?
c) Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn
Theo dõi (0) 1 Trả lời -


Bài 75 trang 169 sách bài tập Toán 9 tập 1
bởi Tuấn Huy
 04/01/2019
Bài 75 (Sách bài tập trang 169)
04/01/2019
Bài 75 (Sách bài tập trang 169)Cho đường tròn (O; 3cm) và đường tròn (O'; 1cm) tiếp xúc ngoài tại A. Vẽ hai bán kính OB, O'C song song với nhau thuộc cùng một nửa mặt phẳng có bờ OO'
a) Tính số đo góc BAC
b) Gọi I là giao điểm của BC và OO'. Tính độ dài OI ?
Theo dõi (0) 1 Trả lời -


Bài 74 trang 169 sách bài tập Toán 9 tập 1
bởi Nguyễn Thị An
 04/01/2019
Bài 74 (Sách bài tập trang 169)
04/01/2019
Bài 74 (Sách bài tập trang 169)Cho hai đường tròn đồng tâm O. Một đường tròn (O') cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D.
Chứng minh rằng AB // CD ?
Theo dõi (0) 1 Trả lời -


Bài 73 trang 169 sách bài tập Toán 9 tập 1
bởi Dương Minh Tuấn
 04/01/2019
Bài 73 (Sách bài tập trang 169)
04/01/2019
Bài 73 (Sách bài tập trang 169)Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn \(\left(C\in\left(O\right),D\in\left(O'\right)\right)\)
a) Tính số đo góc CAD
b) Tính độ dài CD biết OA = 4,5, O'A = 2cm
Theo dõi (0) 1 Trả lời -


Bài 72 trang 169 sách bài tập Toán 9 tập 1
bởi Nguyễn Thị Thúy
 04/01/2019
Bài 72 (Sách bài tập trang 169)
04/01/2019
Bài 72 (Sách bài tập trang 169)Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lởn C và D ( A nằm giữa B và C). So sánh các độ dài Ac và BD ?
Theo dõi (0) 1 Trả lời





