Bài tập 44 tr 107 sách BT Toán lớp 9 Tập 2
Vẽ hình vuông \(ABCD\) tâm \(O\) rồi vẽ tam giác đều có một đỉnh là \(A\) và nhận \(O\) làm tâm. Nêu cách vẽ.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Hình vuông là có hai đường chéo bằng nhau, cắt nhau tại trung điểm mỗi đường, và hai đường chéo vuông góc với nhau.
+) Tam giác đều có các cạnh, các góc bằng nhau bằng \(60^\circ.\)
+) Bất kì đa giác nào cũng có một và chỉ một đường tròn ngoại tiếp.
Lời giải chi tiết
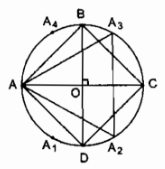
Cách vẽ:
− Vẽ đường tròn (O; R)
− Kẻ 2 đường kính AC ⊥ BD
− Nối AB, BC, CD, DA ta được tứ giác ABCD là hình vuông nội tiếp trong đường tròn (O; R)
− Từ A đặt liên tiếp các cung bằng nhau có dây trương cung bằng bán kính R.
\(\overparen{{A}{A_1}}\), \(\overparen{{A_1}{A_2}}\), \(\overparen{{A_2}{C}}\), \(\overparen{{C}{A_3}}\), \(\overparen{{A_3}{A_4}}\)
Nối AA2; A2A3; A3A ta có ∆AA2A3 là tam giác đều nhận O làm tâm.
-- Mod Toán 9 HỌC247
-


Chứng minh AC là phân giác của góc BAE
bởi Nguyễn Thanh Trà
 10/01/2019
10/01/2019
Cho đường tròn đường kính AB. Qua C thuộc nửa đường tròn kẻ tiếp tuyến d với đường tròn. Gọi E, F lần lượt là chân đường vuông góc kẻ từ A, B đến d và H là chân đường vuông góc kẻ từ C đến AB. Chứng ming
a/ CE=fc
b/AC là phân giác của góc BAE
c/CH2=BF. AE
Theo dõi (0) 1 Trả lời -


Cho hai đường tròn (O) và (O') tiếp xúc nhau tại A. Qua A vẽ một cát tuyến cắt đường tròn (O) và (O') tại B và C. Vẽ tiếp tuyến Bx của đường tròn (O) và tiếp tuyến Cy của đường tròn (O'). Chứng minh By//Cy
Theo dõi (0) 1 Trả lời -


Chứng minh rằng AMCD và MADE nội tiếp
bởi Xuan Xuan
 24/01/2019
24/01/2019
Giúp tớ với ạ cần gấp tks ạ !!!!
1) Cho nửa đường tròn đường kính AB,tia tiếp tuyến Ax (cùng phía đtròn). Từ M trên tia Ax kẻ tiếp tuyến MC vs nửa đtròn. AC cắt OM tại B, MB cắt nửa đtròn (O) tại D
A) c/m t/g AMCD và MADE nội tiếp
B) c/m góc ADE = góc ACO
C) Vẽ CH vuông góc AB (h €AB) c/m MB đi qua trung điểm CH
Theo dõi (0) 1 Trả lời -


Chứng minh ABOC ngoại tiếp đường tròn
bởi Nguyễn Trà Giang
 11/01/2019
11/01/2019
Từ điểm A ở ngoài đường trong (O), kẻ hai tiếp tuyến AB,AC tới đường tròn ( B,C là các tiếp điểm ). Đường thẳng qua A cắt đường tròn (O) tại D và E( D nằm giữa A và E, dây DE không qua tâm O ). Gọi H là trung điểm của DE, AE cắt BC tại K.
a) C/m ABOC nt đường tròn .
b) C/m HA là tia phân giác của góc BHC
c ) Chứng minh : \(\dfrac{2}{AK}=\dfrac{1}{AD}+\dfrac{1}{AE}\)
D ) Đường thẳng kẻ qua D vuông góc OB cắt BE tại F, cắt BC ở I. Chứng minh : ID = IF
Theo dõi (0) 1 Trả lời -


Cho nửa đương tròn tâm (O), đương kính AB. Lấy điểm C thuộc nửa đương tròn (O) và điểm D trên đương kính AB ( C và D khác A, B). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn (O), vẽ các tiếp tuyến Ax và By. Đường thẳng đi qua C và vuông góc vối CD cắt Ax, By lần lượt tại E, F.
a) Tứ giác ADCE nội tiếp trong một đương tròn
b) tam giác EDF vuông
c) MN // AB
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD cân
bởi Long lanh
 14/01/2019
14/01/2019
Cho đường tròn (O)đường kính AB. Kẻ tiếp tuyến Ax với đường tròn. Điểm C thuộc nửa đường tròn cùng nửa mặt phẳng với Ax với bờ là AB. Phân giác góc CAx cắt đường tròn tại E, cắt BC ở D
a. Chứng minh: Tam giác ABD cân
b. H là giao AC và BE. Chứng minh: \(DH\perp AB\)
c. BE cắt Ax tại K. Chứng minh: AKDH là hình thoi
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác BCKM nội tiếp và OM=OK
bởi Dell dell
 14/01/2019
14/01/2019
Cho nửa (O) đường kính AB . Gọi C là trung điểm của OA , đường thằng d vuông góc với AB tại C cắt nửa (O) tại I . K là một điểm thuộc đonạ thẳng CI , tia AK cắt nửa (O) tại M , BM cắt d tại n. Tiếp tuyến tại M của nửa (O) cắt d tại Q . Chứng minh:
a) Tứ giác BCKM nội tiếp và OM=OK
b) Khi K di động trên đoạn IC thì tâm của đường tròn ngoại tiếp tam giác AKN luôn thuộc 1 đường thẳng cố định
HEPL ME GIÚP MK VS CÁC CẬU> THANK TRC NHA
Theo dõi (0) 1 Trả lời -


Giải phương trình căn(2x^2-7x+4)= x-2
bởi Chai Chai
 14/01/2019
14/01/2019
Giải phương trình
√2x2-7x+4 = x-2
Theo dõi (0) 1 Trả lời -


Chứng minh K, Q, B thẳng hàng
bởi minh vương
 14/01/2019
14/01/2019
Cho nửa đường tròn đường kính AB = 2R, M là một điểm trên đường tròn đó sao cho MA > MB. Trên tia BM lấy điểm P sao cho MP = MA. Đường thẳng vuông góc với AB vẽ từ P cắt AB tại H và cắt MA tại Q, AP cắt nửa đường tròn tại K.
1. Chứng minh:
a/ K, Q, B thẳng hàng
b/ \(\Delta MQB\) vuông cân
c/ Q là tâm đường tròn nội tiếp \(\Delta KHM\)
2. Cho góc MAB = 300. Tính diện tích \(\Delta ABP\) theo R
Theo dõi (0) 1 Trả lời -


cho (O:R) AB=2R. dây cung CD cắt AB tại M. biết Mc =4 ,MD=12. góc BMD= 30 độ .
a, tính khoảng cách từ O đến CD
b,tính R
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MBA đều và tính diện tích theo R
bởi Duy Quang
 14/01/2019
14/01/2019
Cho đường tròn (O; R) và M là một điểm sao cho OM=2R.
Từ M, kẻ hai tiếp tuyến MA, MB với đường tròn (A,B là các tiếp điểm, A khác B)
a) Tính MA theo R
b) CM: Tam giác MBA đều và tính diện tích theo R
c) Gọi N là điểm thuộc cung nhỏ AB. Vẽ tiếp tuyến với đường tròn (O) cắt các tiếp tuyến MA, MB theo thứ tự ở C và D. Tính tỉ số chu vi của hai tam giác MCD và MAB
d) Gọi H là giao điểm của AB và MO, đường thẳng MO cắt đường tròn (O) tại P và Q (P nằm giữa M và O). CM: MP.MQ = MH.MO
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác BDE cân
bởi Nguyễn Bảo Trâm
 14/01/2019
14/01/2019
Cho (O), vẽ dây AB khác đường kính. Lấy điểm C trên cung lớn AB sao cho tia AC cắt tiếp tuyến tại B của (O) ở D. Đường tròn đi qua ba điểm B, C, D cắt đường thẳng AB tại điểm thứ hai là E. Chứng minh tam giác BDE cân.
Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác MAOB ngoại tiếp
bởi hồng trang
 14/01/2019
14/01/2019
Cho đường tròn tâm O,từ điểm bên ngoài đường tròn kẻ hai tiếp tuyến MA,MB với đường tròn.Vẽ cát tuyến MCD của (O)(C nằm giữa M và D)
a)CM: Tứ giác MAOB nt
b)CM:MA2 =MC.MD
c)Giả sử bán kính của (O) là 6cm,OM=10cm,CD=3,6cm.Tính MD
Giúp mình câu c nhé !Mình sắp thi tuyển sinh rồi.Thank nhìu!
Hình vẽ ở dưới đây các bạn xem nhé!
Hình mình vẽ hơi xấu nên các bạn thông cảm cho mình!
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 63 trang 92 SGK Toán 9 Tập 2
Bài tập 64 trang 92 SGK Toán 9 Tập 2
Bài tập 45 trang 107 SBT Toán 9 Tập 2
Bài tập 46 trang 107 SBT Toán 9 Tập 2
Bài tập 47 trang 108 SBT Toán 9 Tập 2
Bài tập 48 trang 108 SBT Toán 9 Tập 2
Bài tập 49 trang 108 SBT Toán 9 Tập 2
Bài tập 50 trang 108 SBT Toán 9 Tập 2
Bài tập 51 trang 108 SBT Toán 9 Tập 2





