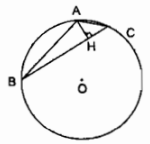
Bài tập 50 tr 108 sách BT Toán lớp 9 Tập 2
Trong đường tròn \((O; R)\) cho một dây \(AB\) bằng cạnh hình vuông nội tiếp và dây \(BC\) bằng cạnh tam giác đều nội tiếp (điểm \(C\) và điểm \(A\) ở cùng một phía đối với \(BO\)). Tính các cạnh của tam giác \(ABC\) và đường cao \(AH\) của nó theo \(R.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
Lời giải chi tiết
Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O; R) nên AB = \(R\sqrt 2 \) và cung \(\overparen{AB}\) nhỏ có sđ \(\overparen{AB}\).
Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O; R) nên BC = \(R\sqrt 3 \) và cung nhỏ \(\overparen{BC}\) nhỏ có sđ \(\overparen{BC}\) \( = 120^\circ \).
\( \Rightarrow \) sđ \(\overparen{AC}\) = sđ \(\overparen{BC}\) - sđ \(\overparen{AB}\) = \(120^\circ - 90^\circ = 30^\circ \)
\( \Rightarrow \widehat {ABC} = {1 \over 2}\) sđ \(\overparen{AC}\) = 150(tính chất góc nội tiếp)
Trong ∆AHB có \(\widehat {AHB} = 90^\circ \)
\( \Rightarrow AH = AB.\sin \widehat {ABH} = R\sqrt 2 .\sin 15^\circ \approx 0,36R\)
Trong ∆AHC có \(\widehat {AHC} = 90^\circ \)
\widehat {ACB} = {1 \over 2}\) sđ \(\overparen{AB}\) = 450 (tính chất góc nội tiếp)
\(AC = {{AH} \over {\sin \widehat {ACH}}} = {{AH} \over {\sin 45^\circ }} \approx {{0,36R} \over {\sin 45^\circ }} \approx 0,51R\)
-- Mod Toán 9 HỌC247
-


Bài 71 trang 168 sách bài tập Toán 9 tập 1
bởi hà trang
 04/01/2019
Bài 71 (Sách bài tập trang 168)
04/01/2019
Bài 71 (Sách bài tập trang 168)Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I; IA) và (B; BA)
a) Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào đối với nhau ? Vì sao ?
b) Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại M và N. So sánh các độ dài AM và MN ?
Theo dõi (0) 1 Trả lời -


Bài 8.2 trang 109 sách bài tập toán 9 tập 2
bởi Lê Nguyễn Hạ Anh
 08/10/2018
08/10/2018
Bài 8.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 109)
Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB với đường tròn (O). Qua điểm M kẻ cát tuyến MCD với đường tròn (O), tức là đường thẳng đi qua điểm M và cắt đường tròn tại hai điểm là C, D). Gọi I là trung điểm của dây CD, Khi đó MAOIB có là ngũ giác nội tiếp hay không ?
Theo dõi (0) 1 Trả lời -


Bài 8.1 trang 109 sách bài tập toán 9 tập 2
bởi thu trang
 08/10/2018
Bài 8.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 109)
08/10/2018
Bài 8.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 109)Mỗi câu sau đây đúng hay sai ?
a) Mỗi tam giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
b) Mỗi tứ giác luôn có một đường tròn ngoại tiếp và một đường tròn nội tiếp
c) Giao điểm ba đường trung tuyến của một tam giác là tâm đường tròn ngoại tiếp tam giác ấy
d) Giao điểm ba đường trung trực của một tam giác là tâm đường tròn nội tiếp tam giác ấy
e) Giao điểm ba đường phân giác của một tam giác là tâm đường tròn nội tiếp tam giác ấy
f) Giao điểm ba đường cao của một tam giác là tâm đường tròn nội tiếp tam giác ấy
g) Tứ giác có tổng độ dài các cặp cạnh đối bằng nhau thì ngoại tiếp được đường tròn
h) Tứ giác có tổng số đo các cặp góc (trong) đối nhau bằng nhau thì nội tiếp được đường tròn
i) Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó
Theo dõi (0) 1 Trả lời -


Bài 51 trang 108 sách bài tập toán 9 tập 2
bởi Dell dell
 08/10/2018
08/10/2018
Bài 51 (Sách bài tập - tập 2 - trang 108)
Cho ngũ giác đều ABCDE. Gọi I là giao điểm của AD và BE. Chứng minh \(DI^2=AI.AD\)
Hướng dẫn : Vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE rồi xét hai tam giác đồng dạng AIE và AED
Theo dõi (0) 1 Trả lời -


Bài 50 trang 108 sách bài tập toán 9 tập 2
bởi thi trang
 08/10/2018
08/10/2018
Bài 50 (Sách bài tập - tập 2 - trang 108)
Trong đường tròn (O; R) cho một dây AB bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp (điểm C và điểm A ở cùng một phía đối với BO). Tính các cạnh của tam giác ABC và đường cao AH của nó theo R
Theo dõi (0) 1 Trả lời -


Bài 26 trang 169 sách bài tập Toán 9 tập 2
bởi Anh Trần
 04/01/2019
Bài 26 (Sách bài tập - tập 2 - trang 169)
04/01/2019
Bài 26 (Sách bài tập - tập 2 - trang 169)Hình 101 :
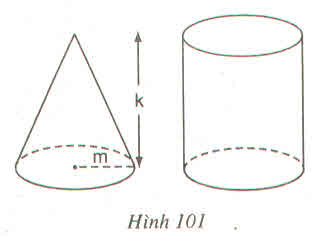
Có một hình nón, chiều cao k (cm), bán kính đường tròn đáy m(cm) và một hình trụ có cùng chiều cao và bán kính đường tròn đáy với hình nón. Chứa đầy cát vào hình nón rồi đổ hết vào hình trụ thì độ cao của cát trong hình trụ sẽ là :
(A) \(\dfrac{k}{4}cm\) (B) \(\dfrac{k}{3}cm\)
(C) \(\dfrac{2k}{3}cm\) (D) \(\dfrac{3k}{4}cm\)
Hãy chọn kết quả đúng ?
Theo dõi (0) 1 Trả lời -


Bài 23 trang 168 sách bài tập Toán 9 tập 2
bởi Nguyễn Thị Lưu
 04/01/2019
Bài 23 (Sách bài tập - tập 2 - trang 168)
04/01/2019
Bài 23 (Sách bài tập - tập 2 - trang 168)Hình 99 là một hình nón :
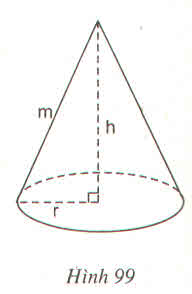
Chiều cao h (cm), bán kính đường tròn đáy là r (cm) và độ dài đường sinh m(cm) thì thể tích hình nón này là :
(A) \(\pi r^2h\left(cm^3\right)\) (B) \(\dfrac{1}{3}\pi r^2h\left(cm^3\right)\)
(C) \(\pi rm\left(cm^3\right)\) (D) \(\pi r\left(r+m\right)\left(cm^3\right)\)
Hãy chọn kết quả đúng ?
Theo dõi (0) 1 Trả lời -


Bài II.3 trang 172 sách bài tập Toán 9 tập 1
bởi Duy Quang
 04/01/2019
Bài II.3 - Bài tập bổ sung (Sách bài tập trang 172)
04/01/2019
Bài II.3 - Bài tập bổ sung (Sách bài tập trang 172)Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB
a) Chứng minh rằng 3 điểm M, H,O thẳng hàng
b) Tứ giác AOBH là hình gì ?
c) Khi M di chuyển trên xy thì H di chuyển trên đường nào ?
Theo dõi (0) 1 Trả lời -


Bài 20 trang 168 sách bài tập Toán 9 tập 2
bởi Lê Nhi
 04/01/2019
Bài 20 (Sách bài tập - tập 2 - trang 168)
04/01/2019
Bài 20 (Sách bài tập - tập 2 - trang 168)Hình 98:
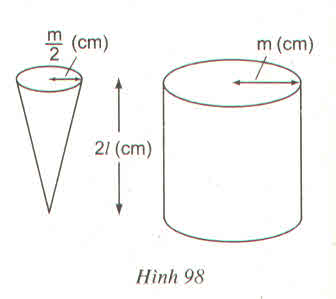
Có một hình nón, bán kính đường tròn đáy là \(\dfrac{m}{2}\left(cm\right)\), chiều cao là 2l (cm) và một hình trụ, bán kính đường tròn đáy m(cm), chiều cao 2l (cm). Người ta mức đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là :
(A) \(\dfrac{l}{6}\left(cm\right)\)
(B) \(l\left(cm\right)\)
(C) \(\dfrac{5}{6}l\left(cm\right)\)
(D) \(\dfrac{11}{6}l\left(cm\right)\)
Hãy chọn kết quả đúng ?
Theo dõi (0) 1 Trả lời -


Bài II.2 trang 172 sách bài tập Toán 9 tập 1
bởi Nguyễn Trung Thành
 04/01/2019
Bài II.2 - Bài tập bổ sung (Sách bài tập trang 172)
04/01/2019
Bài II.2 - Bài tập bổ sung (Sách bài tập trang 172)Cho nửa đường tròn (O) đường kính AB. Trên nủa mặt phẳng bờ AB chứa nửa đường tròn , vẽ các tia tiếp tuyến Ax và By với nửa đường tròn. Gọi M là điểm thuộc nửa đường tròn, D là giao điểm của AM và By, C là giao điểm của BM và Ax, E là trung điểm của BD. Chứng minh rằng :
a)\(AC.BD=AB^2\)
b) ME là tiếp tuyến của nửa đường tròn
Theo dõi (0) 1 Trả lời -


Xác định các góc tam giác ABC biết BD = 2AM
bởi Thuy Kim
 14/02/2019
14/02/2019
Cho tam giác ABC cân tại A, vẽ trung tuyến AM và đường phân giác BD. Xác định các góc tam giác ABC biết BD = 2AM
Theo dõi (0) 1 Trả lời -


Chứng minh BC là tiếp tuyến của đường tròn
bởi minh thuận
 21/01/2019
21/01/2019
cho đường tròn (O,6cm) và điểm A ở trên đường tròn. Qua A kẻ tiếp tuyến Ax , trên à lấy điểm B sao cho AB= 8 cm.
a: tính OB (m làm được rồi)
b: Qua A kẻ đường vuông góc với OB, cắt đường tròn ở C. Chứng minh :BC là tiếp tuyến của đường tròn
Theo dõi (0) 1 Trả lời -


Chứng minh rằng đường tròn đường kính HK tiếp xúc BC
bởi Thùy Trang
 21/01/2019
21/01/2019
Cho nửa đường tròn tâm (O) đường kính BC, A là một điểm thuộc nửa dduwwowngf tròn (A khác B,C). Từ A kẻ tiếp tuyến d với đường tròn tâm (O). Kẻ BH,CK cùng vuông góc với d (H,K thuộc d)
a)CM: đường tròn đường kính HK tiếp xúc BC
b) Xác định vị trí của điểm A trên nửa đường tròn để diện tích tứ giác BHKC có diện tích lớn nhất. Tính diện tích lớn nhất đó theo BC
c) Gọi M là tiếp điểm của BC với đường tròn đường kính HK.CM: khi M nằm giữa B và O thì \(\widehat{MAO}=\frac{\cot\widehat{ACB}-\cot\widehat{ABC}}{2}\)
Theo dõi (0) 1 Trả lời