Bài tập 51 tr 108 sách BT Toán lớp 9 Tập 2
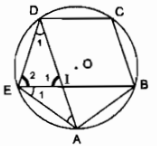
Cho ngũ giác đều \(ABCDE.\) Gọi \(I\) là giao điểm của \(AD\) và \(BE.\) Chứng minh \(D{I^2} = AI.AD\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)
+) Nếu \(C\) là một điểm trên cung \(AB\) thì: \(sđ \overparen{AB}=sđ \overparen{AC}+sđ \overparen{CB}.\)
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải chi tiết
Vẽ đường tròn ngoại tiếp ngũ giác ABCDE
sđ \(\overparen{AB}\) = sđ \(\overparen{BC}\) = sđ \(\overparen{CD}\) = sđ \(\overparen{DE}\) = sđ \(\overparen{AE}\)= 720 (1)
\(\widehat {{E_1}} = {1 \over 2}\) sđ \(\overparen{AB}\) (tính chất góc nội tiếp) (2)
\(\widehat {{D_1}} = {1 \over 2}\) sđ \(\overparen{AE}\) (tính chất góc nội tiếp) (3)
Từ (1), (2) và (3) suy ra: \(\widehat {{E_1}} = \widehat {{D_1}}\)
Xét ∆AIE và ∆AED:
\(\widehat {{E_1}} = \widehat {{D_1}}\) (chứng minh trên)
\(\widehat A\) chung
Suy ra: ∆AIE đồng dạng ∆AED (g.g)
\({{AI} \over {AE}} = {{AE} \over {AD}}\)
\( \Rightarrow \) AE2 = AI. AD (*)
\(\widehat {{E_2}} = {1 \over 2}\) sđ \(\overparen{BCD}\) (tính chất góc nội tiếp) hay \(\widehat {{E_2}} = {1 \over 2}\) (sđ \(\overparen{BC}\) + sđ \(\overparen{CD}\)) (4)
\(\widehat {{I_1}} = {1 \over 2}\) (sđ \(\overparen{DE}\) + sđ \(\overparen{AB}\)) (tính chất góc có đỉnh ở trong đường tròn) (5)
Từ (1), (4) và (5) suy ra: \(\widehat {{E_2}} = \widehat {{I_1}}\)
\( \Rightarrow \) △DEI cân tại D \( \Rightarrow \) DE = DI
DE = AE (gt)
Suy ra: DI = AE (**)
Từ (*) và (**) suy ra: DI2 = AI. AD
-- Mod Toán 9 HỌC247
-


Chứng minh tam giác ABD cân, OE song song với BD
bởi Phạm Phú Lộc Nữ
 21/01/2019
21/01/2019
Cho nửa đường tròn tâm O.Đường kính AB,AC là dây cung của nó.
Tiếp tuyến Ax; phân giác góc CAx giao với BC tại D.AD giao với đường tròn tâm O tại E.
Chứng minh:
a, Tam giác ABD cân. OE song song với BD.
b,AC giao với BE tại I. Chứng minh DI vuông góc với AB.
c,C di động trên nửa đường tròn tâm O thì D chạy trên đường nào
Theo dõi (0) 1 Trả lời -


Chứng minh A,B,O,C cùng thuộc một đường tròn
bởi Nguyễn Bảo Trâm
 21/01/2019
21/01/2019
Cho A nằm ngoài đường tròn tâm O, bán kính R, tiếp tuyến AB, AC (B, C là tiếp điểm)
Chứng minh: A,B,O,C cùng thuộc một đường tròn
Theo dõi (0) 1 Trả lời -


Chứng minh AMB là tam giác đều
bởi ngọc trang
 21/01/2019
21/01/2019
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB= 60 độ
a: Chứng minh AMB là tam giác đều
b: Tính chu vi tam giác AMB
c: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?
Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xy
a: tứ giác APMQ là hình gì? Vì sao?
b: gọi I là trung điểm PQ. Chứng minh OI vuông góc AM
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc B = 90 độ, góc A = 30 độ, BC = 3cm, đường cao BH
a, Tính AB, AC, góc C
b, Tính diện tích tam giác ABH
c, Tính bán kính đường tròn ngoại tiếp tam giác ABC
d, Tính AG ( G là trọng tâm tam giác ABC )Theo dõi (0) 1 Trả lời -


Tính AD,AC VÀ BC theo a
bởi Đào Lê Hương Quỳnh
 21/01/2019
21/01/2019
Cho đoạn thẳng AB= 2a. Từ trung điểm O của AB vẽ tia Ox vuông góc AB. Trên Ox, lấy điểm D sao cho OD=\(\frac{a}{2}\) .Từ B kẻ BC vuông góc với đường thẳng AD
a/ Tính AD,AC VÀ BC theo a
b/ Kéo dài DO một đoạn OE=a. chứng minh bốn điểm A,B,C và E cùng nằm trên một đường tròn
GIÚP VỚI, THANKS NHIỀU
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tính AC, BC, HB, HC, biết AB=7,5cm, AH=6cm
bởi Nguyễn Hạ Lan
 17/01/2019
17/01/2019
Cho tam giác ABC vuông tại A đường cao AH. Biết AB=7,5cm ,AH=6cm
Tính AC,BC,HB,HC.
Theo dõi (0) 1 Trả lời -


Tính các cạnh của tam giác ABC, biết BH=5; CH=12, bán kính đường tròn nội tiếp bằng 6
bởi Lê Nhật Minh
 14/02/2019
14/02/2019
cho tam giác ABC vuông tại A . I là tâm đường tròn nội tiếp tam giác có IH vuông góc với BC biết BH=5; CH=12. bán kính đường tròn nội tiếp bằng 6, một cạnh góc vuông =20. tính các cạnh của tam giác ABC
Theo dõi (0) 1 Trả lời -


Chứng minh M,N,P thẳng hàng
bởi Nguyễn Lê Thảo Trang
 21/01/2019
21/01/2019
Cho tứ giác ABCD nội tiếp đường tròn đường kính BD. Gọi M,N,P lần lượt là hình chiếu của A trên BC,BD,CD. Chứng minh M,N,P thẳng hàng
Theo dõi (0) 1 Trả lời -


Tính bán kính đường tròn ngoại tiếp R và bán kính đường tròn nội tiếp tam giác
bởi thùy trang
 21/01/2019
21/01/2019
cho tam giác ABC vuông tạ A có AB = 6cm, ac = 8cm. Tính bán kính đường tròn ngoại tiếp R và bán kính đường tròn nội tiếp tam giác
Theo dõi (0) 1 Trả lời -


Chứng tỏ AD là đường kính của hình tròn
bởi thu phương
 21/01/2019
21/01/2019
cho tam giác ABC cân tại A nội tiếp đường tròn tâm O đường cao AH cắt đường tròn ở D
a)Chứng tỏ AD là đường kính của hình tròn
b)tính số đo góc ACD
c)Tính đường cao AH,bán kính đường tròn biết AC=20cm,BC=24cm
Theo dõi (0) 1 Trả lời -


Chứng minh góc DAB = góc BDE
bởi Anh Nguyễn
 21/01/2019
21/01/2019
cho hai đường tròn (o1,r1) và (o2,r2) với r1 > r2, cắt nahu tại hai điểm A và B. kẻ tiếp tuyến chung DE củ Hi đường tròn với D thuộc (o1)
và E thuộc (o2) sao cho B gần tiếp tuyến đó hơn so với A
a) chứm minh góDAB = gócBDE
b)Tia AB cắt tia DE tại M . chứng minh rằng M là trung điểm của DE
c) đường thẳng EB cắt AD tại P , đường thảng DB cắt AE tại Q. cmr : PQ // DE.Theo dõi (0) 1 Trả lời -


Chứng minh rằng ABCD là tứ giác nội tiếp
bởi Lê Vinh
 21/01/2019
21/01/2019
* BÀI : cho ΔABC vuông tại A.Trên AC lấy điểm M. Dựng Đường tròn (O) đường kính MC, BM cắt (O) tại D, AD cắt (O) tại S.
1> cm ABCD là tứ giác nội tiếp
2> cm CA là tia phân giác của góc SCB
3> gọi E là giao điểm của BC và (O) , cm BA, EM, CD đồng quy
4> cm DM là tia phân giác của góc ADE
6> cm M là tâm dường tròn nội tiếp ΔADE
ps: mb làm giùm tớ nha thanks các bạn trc
thanks các bạn trc  ai yêu toán add friend fb vs tớ nha =))Theo dõi (0) 1 Trả lời
ai yêu toán add friend fb vs tớ nha =))Theo dõi (0) 1 Trả lời -


Tính khoảng cách OH từ O đến dây BC
bởi Trần Phương Khanh
 21/01/2019
21/01/2019
Cho đường tròn tâm O bán kính 15 cm ,dây BC =24 cm. Các tiếp tuyến của đường tròn tâm O tại B và C cắt nhau tại A.
- Tính khoảng cách OH từ O đến dây BC.
- C/m O,H,A thẳng hàng.
- Tính AB,AC.
- Gọi Mlà giao của AB và CO , N là giao của AC và BO. C/m BCNM là hình thang cân.
Theo dõi (0) 1 Trả lời