Bài tập 8.2 tr 109 sách BT Toán lớp 9 Tập 2
Cho đường tròn tâm \(O\) bán kính \(R\) và điểm \(M\) ở ngoài đường tròn đó. Qua điểm \(M\) kẻ hai tiếp tuyến \(MA,\) \(MB\) với đường tròn \((O).\) Qua điểm \(M\) kẻ cát tuyến \(MCD\) với đường tròn \((O)\) (tức là đường thẳng đi qua điểm \(M\) và cắt đường tròn tại hai điểm \(C, D).\) Gọi \(I\) là trung điểm của dây \(CD.\) Khi đó \(MAOIB\) có là ngũ giác nội tiếp hay không\(?\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Nếu các đỉnh của đa giác cùng nhìn một cạnh dưới góc vuông thì đa giác đó nội tiếp đường tròn.
Lời giải chi tiết
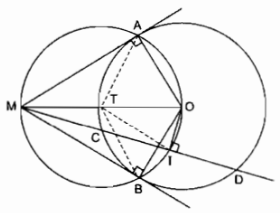
Khi cắt tuyến MCD không đi qua O.
IC = ID (gt)
\( \Rightarrow \) OI ⊥ CD (đường kính đi qua điểm chính giữa của dây không đi qua tâm)
\( \Rightarrow \widehat {MIO} = 90^\circ \)
MA ⊥ OA (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MAO} = 90^\circ \)
MB ⊥ OB (tính chất tiếp tuyến)
\( \Rightarrow \widehat {MBO} = 90^\circ \)
A, I, B nhìn MO dưới một góc bằng 90º nên A, I, B nằm trên đường tròn đường kính MO.
Vậy: Ngũ giác MAOIB nội tiếp.
(Khi cắt tuyến MCD đi qua O ngũ giác MAOIB suy biến thành tứ giác MAOB chứng minh tương tự).
-- Mod Toán 9 HỌC247
-
Chứng minh rằng CH=DK
bởi Lê Tấn Thanh
17/01/2019
Cho đường tròn tâm O đường kính AB. Dây cung CD cắt AB tại I . Gọi H và K lần lượt là chân các đường vuông góc kẻ từ A và B đuến CD. Chứng minh rằng CH=Dk
Theo dõi (0) 1 Trả lời -
Chứng minh tứ giác CEHD nội tiếp, bốn điểm A, E, D, B cùng nằm trên một đường tròn
bởi Mai Trang
17/01/2019
Cho tam giác cân ABC (AB = AC), các đường cao AD, BE, cắt nhau tại H. Gọi O là tâm đường tròn ngoại tiếp tam giác AHE.
- Chứng minh tứ giác CEHD nội tiếp .
- Bốn điểm A, E, D, B cùng nằm trên một đường tròn.
- Chứng minh ED = 1/2BC.
- Chứng minh DE là tiếp tuyến của đường tròn (O).
- Tính độ dài DE biết DH = 2 Cm, AH = 6 Cm
Theo dõi (0) 1 Trả lời -
Chứng minh CE=CF
bởi het roi
17/01/2019
cho 1/2 (o0 đường kính AB, qua điểm C thuộc nửa đường tròn ta kẻ tiếp tuyến d. Gọi E và F lần lượt là các chân đường vuong góc, kẻ từ A và B đến d. Vẽ OH vuông góc với AB. Chứng minh:
a) CE=CF
b)AC là tia phân giác của góc BAE
c) CH^2 = AE*BF
Theo dõi (0) 1 Trả lời -
Tính các cạnh và đường cao của tam giác ABC
bởi Vũ Hải Yến
17/01/2019
Cho tam giác ABC.Các đường cao là các số tự nhiên.Bán kính đường tròn nội tiếp = 1.Tính các cạnh và đường cao của tam giác ABC.
Theo dõi (0) 1 Trả lời -
Chứng minh E,H,F thẳng hàng
bởi Hoàng My
17/01/2019
Cho tam giác ABC nhọn nội tiếp đường tròn (O); đường cao CP,BN cắt nhau tại H. Q thuộc cung nhỏ BC; E,F lần lượt đối xứng với Q qua AB,AC. Chứng minh: E,H,F thẳng hàng
Theo dõi (0) 1 Trả lời -
Chứng minh hệ thức BM.CN=BN.CM
bởi A La
17/01/2019
Cho đường tròn tâm O và một điểm A nằm ngoài đường tròn.Từ A kẻ hai tiếp tuyến AB,AC và cát tuyến AMN với đường tròn (B,C,M,N thuộc đường tròn và AM<AN).
a) Chứng minh hệ thức BM.CN=BN.CM
b) Gọi E là trung điểm của dây MN,tia CE cắt đường tròn tại điểm thứ hai D. Chứng minh rằng BD//MN
c)Xác định vị trí cát tuyến AMN để diện tích tam giác ADN lớn nhấtTheo dõi (0) 1 Trả lời -
Tìm tập hợp các điểm I khi A di động biết tam giác ABC vuông ở A, có cạnh BC cố định
bởi Ngô Vân
06/02/2018
Cho tam giác ABC vuông ở A, có cạnh BC cố định . Điểm I là giao điểm của 3 đường phân giác trong. Tìm tập hợp các điểm I khi A di động , góc BIC bằng bao nhiêu
Theo dõi (2) 1 Trả lời
