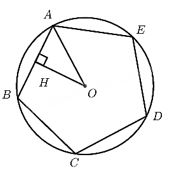
Bài tập 48 tr 108 sách BT Toán lớp 9 Tập 2
\(a)\) Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(3cm.\)
\(b)\) Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính \(3cm.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)
Lời giải chi tiết
\(a)\) Kẻ \(OH ⊥ AB,\) ta có: \(HA = HB = \displaystyle {1 \over 2}AB,OA = R = 3cm\)
Vì \(ABCDE\) là ngũ giác đều nên: \(\widehat {BOA} = \displaystyle{{360^\circ } \over 5} = 72^\circ \)
Suy ra \(\widehat {HOA} =\dfrac{\widehat{BOA}}{2}\)\(= \displaystyle{{72^\circ } \over 5} = 36^\circ \)
Trong tam giác vuông \(OHA\) vuông tại \(H\) ta có:
\(AH = OA.\sin \widehat {HOA}\)
\( \Rightarrow AB = 2.AH=2OA.\sin \widehat {HOA}\)\( = 2.3.\sin 36^\circ \approx 3,522\) \((cm)\)
\(b)\) Từ giả thiết suy ra \(OH = r = 3 cm\)
Trong tam giác vuông \(OHA\) vuông tại \(H\) ta có:
\(AH = OH.\tan \widehat {HOA}\) \( \Rightarrow AB =2.AH= 2.OH.\tan \widehat {HOA}\)\( = 2.3.\tan 36^\circ \approx 4,356\) \((cm)\)
-- Mod Toán 9 HỌC247
-


Chứng minh rằng IECB nội tiếp
bởi Nguyễn Hoài Thương
 16/01/2019
16/01/2019
Cho đường tròn (O) đường kính AB cố định, điểm I nằm giữa A và O. Kẻ dây MN\(\perp\)AB tại I. Gọi C là điểm tùy ý thuộc \(\stackrel\frown{MC}\) (C không trùng với M, N và B). Nối AC cắt MN tại E
a) Cm IECB nội tiếp
b) Cm \(\Delta AME\) đồng dạng với \(\Delta ACM\) .Chứng minh CM=AM2=AE.AC
Theo dõi (0) 1 Trả lời -


Tính MH và bán kính R
bởi Nguyễn Thủy Tiên
 18/01/2019
18/01/2019
Ai giúp mình với. Cần gấp ạ!!!!
Tam giác AMB cân tại M nội tiếp đường tròn tâm O, bán kính R. Kẻ MH vuông góc với AB, MH cắt đường tròn tại N. Biết MA = 10cm, AB= 12cm
a) Tính MH và bán kính R
b) Trên tia đối BA lấy điểm C, MC cắt đường tròn tại D, ND cắt AB tại E. Chứng minh tứ giác MDEH nội tiếp và các hệ thức: NB2 = NE . ND và AC.BE = BC.AE
c) Chứng minh NB tiếp xúc với đường tròn ngoại tiếp tam giác BDE
Theo dõi (0) 1 Trả lời -


Mn giúp mình giải bài này với ạ .....Cảm ơn nhiều ạ
Từ một điểm A nằm ngoài đường tròn (O0) bán kính R> Kẻ 2 tiếp tuyến AM và AN với đường tròn( M,N là các tiếp điểm)
a) C/M rằng: 4 điểm A,M,O,N cùng thuộc 1 đường tròn
b) Gọi H là giao điểm của OA và MN. Biết OA=2R. Tính AH, OH theeo R
c) Từ A kẻ cát tuyến ABC bất kì ( B nằm giữa A và C ), tiếp tuyến tại B của đường tròn (O) cắt AM,AN theo thứ tự tại P và Q. Qua điểm O kẻ đường thẳng vuông góc với OA cắt tia AM tại I và cắt tia AN tại K. C/M rằng: IP + KQ > IK
Theo dõi (0) 1 Trả lời -


Chứng minh 5 điểm S,A,O,I,B cùng thuộc đường tròn
bởi Đào Thị Nhàn
 16/01/2019
16/01/2019
cho đường tròn (O;R) và điểm S sao cho SO=2R. vẽ các tiếp tuyến SA,SB của dường tròn (O;R) (A;Blà các tiếp điểm) và cát tuyến SMN( không qua O) . Gọi I là trung điểm của MN.
a, Chứng minh 5 điểm S,A,O,I,B cùng thuoojc1 đường tròn
b, chứng minh SA2 = SM.SN
c, Tính SM,SN theo R khi MN=SA
d, Kẻ MH vuông góc OA ,MH cắt AN, AB tại D,E. chứng minh tứ giác IEMB nội tiếp được đường tròn.
Bạn nào biết giải dùm mình bài này với, mình cảm ơn ạ
Theo dõi (0) 1 Trả lời -


Tính số đo cung AB, cho AB=Rcăn3
bởi hà trang
 16/01/2019
16/01/2019
cho AB=\(R\sqrt{3}\) là dây cung của đường tròn (O;R). Tính số đo cung AB
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AKO cân
bởi Trịnh Lan Trinh
 29/01/2019
29/01/2019
Cho (O; R lấy điểm A cách O một khoảng 2R. Kẻ tiếp tuyển AB, AC với đtron. Đoạn thẳng OA cắt (0) tại I. Đường thẳng qua O và vuông góc OB cắt AC tại K .
a) Chứng minh tam giác AKO cân
b) Đường thẳng KI cắt AB tại M. Chứng minh KM là tiếp tuyến của (0)
Theo dõi (0) 1 Trả lời -


Chứng minh AB . CD = BD . AK
bởi Anh Nguyễn
 18/01/2019
18/01/2019
cho bốn điểm A B C D theo thứ tự trên đường tròn tâm 0 . Trên AC lấy điểm K sao cho góc ABK = góc CBD
chứng mih
a. AB . CD = BD . AK
b. BD . AC = BC . AD + AB .CD
Theo dõi (0) 1 Trả lời -


Cho đường tròn tâm O, bán kính R và đường thẳng d không có điểm chung với đường tròn O, H là hình chiếu vuông góc của O trên d. Từ điểm M bất kỳ trên d (M khác H), vẽ hai tiếp tuyến MA, MB tới đường tròn O (A,B là hai tiếp điểm). Gọi K,I thứ tự là giao điểm của AB với OM và OH.
1.Cm: AB=2AK và 5 điểm M,A,O,B,H cùng thuộc một đường tròn
2. Cm OI . OH = OK . OM = R .R
3. Trên đoạn OA lấy điểm N sao cho AN=2ON. Đường trung trực của BN cắt OM ở E. Tính tỉ số OE/OM
Theo dõi (0) 1 Trả lời -


Bài II.1 trang 172 sách bài tập toán 9
bởi Mai Trang
 04/01/2019
Bài II.1 - Bài tập bổ sung (Sách bài tập trang 172)
04/01/2019
Bài II.1 - Bài tập bổ sung (Sách bài tập trang 172)Tỉ số bán kính đường tròn nội tiếp và đường tròn ngoại tiếp một tam giác đều bằng
(A) \(\dfrac{1}{3}\) (B) \(\dfrac{1}{2}\) (C) \(\dfrac{1}{\sqrt{2}}\) (D) \(2\)
Hãy chọn phương án đúng ?
Theo dõi (0) 1 Trả lời -


Bài 88 trang 171 sách bài tập Toán 9 tập 1
bởi thu thủy
 04/01/2019
Bài 88 (Sách bài tập trang 171)
04/01/2019
Bài 88 (Sách bài tập trang 171)Cho nửa đường tròn O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M( C và D là các tiếp điểm khác H)
a) Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi
Theo dõi (0) 1 Trả lời -


Bài 87 trang 171 sách bài tập Toán 9 tập 1
bởi Mai Thuy
 04/01/2019
Bài 87 (Sách bài tập trang 171)
04/01/2019
Bài 87 (Sách bài tập trang 171)Cho hai đườngtròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.
a) Chứng minh rằng tứ giác DBCE là hình thoi
b) Gọi I là giao điểm của EC và đường tròn (O'). Chứng minh rằng ba điểm D, A, I thẳng hàng
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
Theo dõi (0) 1 Trả lời -


Bài 86 trang 171 sách bài tập Toán 9 tập 1
bởi Thu Hang
 04/01/2019
Bài 86 (Sách bài tập trang 171)
04/01/2019
Bài 86 (Sách bài tập trang 171)Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
a) Hai đường tròn (O) và (O') có vị trí tương đối như thế nào đối với nhau ?
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì ? Vì sao ?
c) Gọi K là giao điểm của DB và đường tròn (O'). Chứng minh rằng ba điểm E, C, K thẳng hàng ?
d) Chứng minh rằng HK là tiếp tuyến của đường tròn (O')
Theo dõi (0) 1 Trả lời -


Bài 85 trang 171 sách bài tập Toán 9 tập 1
bởi Thùy Trang
 04/01/2019
Bài 85 (Sách bài tập trang 171)
04/01/2019
Bài 85 (Sách bài tập trang 171)Cho đường tròn (O), đường kính AB, điểm M thuộc đường tròn. Vẽ điểm N đối xứng với A qua M. BN cắt đường tròn ở C. Gọi E là giao điểm của AC và BM
a) Chứng minh rằng \(NE\perp AB\)
b) Gọi F là điểm đối xứng với E qua M. Chứng minh rằng FA là tiếp tuyến của đường tròn (O)
c) Chứng minh rằng FN là tiếp tuyến của đường tròn (B; BA)
Theo dõi (0) 1 Trả lời