Bài tập 46 tr 107 sách BT Toán lớp 9 Tập 2
Cho một đa giác đều \(n\) cạnh có độ dài mỗi cạnh là \(a.\) Hãy tính bán kính \(R\) của đường tròn ngoại tiếp và bán kính \(r\) của đường tròn nội tiếp đa giác đều đó.
Hướng dẫn:
Tính \(\widehat {COB}\) rồi tính \(\sin \widehat {COB}\) và \(\tan\widehat {COB},\) từ đây tính được \(R\) và \(r\) \((h.4).\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)
Lời giải chi tiết
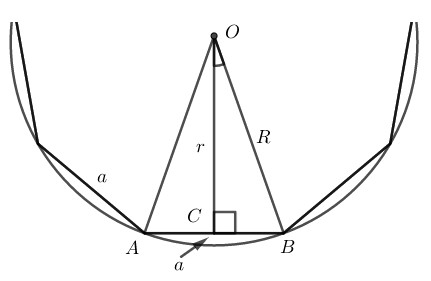
Giả sử một đa giác đều \(n\) cạnh có độ dài một cạnh là \(a.\) Gọi \(R\) là bán kính đường tròn ngoại tiếp, \(r\) bán kính đường tròn nội tiếp.
\( \Rightarrow OB = R; OC = r\)
\(\widehat {AOB} = \displaystyle{{360^\circ } \over n}\)
\( \Rightarrow \widehat {COB} = \displaystyle{{360^\circ } \over n}:2 = {{180^\circ } \over n}\)
Trong \(∆OCB\) ta có: \(\widehat {OCB} = 90^\circ \)
Nên \(\sin \widehat {COB} = \displaystyle{{CB} \over {OB}} = {\displaystyle{{a \over 2}} \over R} = {a \over {2R}}\)
\( \Rightarrow 2R = \displaystyle{a \over {\sin \displaystyle{{180^\circ } \over n}}}\)
\(\Rightarrow R =\displaystyle {a \over {2\sin \displaystyle{{180^\circ } \over n}}}\)
Xét tam giác \(OCB\) vuông tại \(C\), ta có:
\(\tan \widehat {COB} = \displaystyle{{CB} \over {OC}} = {\displaystyle{{a \over 2}} \over r} = \displaystyle{a \over {2r}} \)
\(\Rightarrow 2r = \displaystyle{a \over {\tan \displaystyle{{180^\circ } \over n}}}\)
\(\Rightarrow r = \displaystyle{a \over {2\tan \displaystyle{{180^\circ } \over n}}}\)
-- Mod Toán 9 HỌC247
-


Tính bán kính của đường tròn biết BC=3cm
bởi Trần Phương Khanh
 15/01/2019
15/01/2019
Bài 1 : cho hình thang ABCD có AB// CD (AB<CD) CD=2AD, tính góc C = 60°.
Cm. ABCD cùng nằm trên 1 đường tròn. Tính bán kính của đường tròn biết BC=3cm
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác BANC nội tiếp
bởi hi hi
 15/01/2019
15/01/2019
Cho tam giác ABC vuông tại A, điểm M thuộc AC. Vẽ đường tròn O đường kính MC cắt BC tại E. Nối BM cắt đường tròn O tại N. Nói AN cắt đường tròn O tại D. Lấy I đối xứng với M qua A, K đối xứng với M qua E. Chứng minh:
a. Tứ giác BANC nội tiếp.
b. CA là phân giác của góc BCD
c. ABED là hình thang.
d. Tìm vị trí của M để đường tròn ngoại tiếp tam giác BIK có bán kính R nhỏ nhất.Theo dõi (0) 1 Trả lời -


Chứng minh tứ giác CDIK nội tiếp
bởi Nguyễn Trung Thành
 15/01/2019
15/01/2019
Cho đường tròn O và O' cắt nhau tại A, B ( O và O' thuộc 2 nửa mặt phẳng bờ AB). Qua B kẻ cát tuyến CD vuông góc với AB ( C thuộc đường tròn O, D thuộc đường tròn O'). Tia CA cắt đường tròn O' tại I, tia DA cắt đường tròn O ở K. Chứng minh:
a. Tứ giác CDIK nội tiếp
b. Gọi M là giao điểm của CK và DI. Chứng minh 3 điểm A,M,B thẳng hàng.
Theo dõi (0) 1 Trả lời -


Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn
bởi hi hi
 15/01/2019
15/01/2019
(3,5 điểm) Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.
1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.
2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và vuông góc với BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.
3) Chứng minh H là trực tâm tam giác ABC
4) Khi đường thẳng d thay đổi và thỏa mãn điều kiện của đề bài, điểm H di động trên đường nào
Giúp mình với ạ!
Theo dõi (0) 1 Trả lời -


Chứng minh rằng các điểm M, N, P lần lượt là tâm của đường tròn nội tiếp tam giác ADF, BDE, CEF
bởi minh thuận
 26/01/2019
26/01/2019
Cho tam giác ABC ngoại tiếp đường tròn (O). Gọi D, E, F theo thứ tự là tiếp điểm của đường tròn trên các cạnh AB, BC, AC. Gọi M,N,P lần lượt là giao điểm của đường tròn tâm (O) với các tia OA, OB, OC. Chứng minh rằng các điểm M, N, P lần lượt là tâm của đường tròn nội tiếp tam giác ADF, BDE, CEF.
Các bạn có thể giải hoặc làm sơ đồ ngược để gợi ý cho mình không? Cám ơn trước nhé!
Theo dõi (0) 1 Trả lời -


Chứng minh rằng tứ giác ABMQ nội tiếp
bởi Nguyễn Vũ Khúc
 15/01/2019
15/01/2019
Cho hình vuông ABCD. Gọi M, N là 2 điểm lần lượt trên 2 cạnh BC và CD sao cho góc MAN = 45 độ. AM và AN vắt đường chép DB tại P và Q. Gọi H là giao điểm của MQ và NP. CMR
a. Tứ giác ABMQ nt
b. Tam giác AQM vuông cân
c. AH vuông góc với MN
Theo dõi (0) 1 Trả lời -


Chứng minh rằng MHBI và MHCK nội tiếp
bởi Bo Bo
 15/01/2019
15/01/2019
1. Cho đường tròn tâm O, điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AB,AC. M là điểm bất kì trên BC. Từ M kẻ các đường cao cắt BC,AC,AB tại H,K,I.
a) c/m MHBI và MHCK nội tiếp
b) c/m \(\widehat{MHI}=\widehat{MKH}\)
c) E là giao điểm BM và IH. F là giao điểm HK và MC. c/m EF // BC
2. Cho đường tròn tâm O. Điểm A nằm ngoài. từ A kẻ tiếp tuyến AB,AC. vẽ cát tuyến AMN ( M nằm giữa A,N). I là trung điểm MN
a) c/m ABOC nội tiếp
b) \(AB^2=AM.AN\)
c) Cho T là giao điểm BC và AI. c/m \(\frac{IB}{IC}=\frac{TB}{TC}\)
Ai giúp mình với
Theo dõi (0) 1 Trả lời -


Chứng minh rằng DE^2=AE.AD
bởi Lê Bảo An
 15/01/2019
15/01/2019
Cho AB=2R. Từ B kẻ tia Bx vuông góc với AB, Trên tia Bx lấy o sao cho OB=R. Vẽ đường tròn(O;R). Tia AO cắt (O) tại D và E (D nằm giữa A và E). Dựng đường tròn(A;AD) cắt AB tại C
a) C/M \(DE^2=AE\cdot AD\\ AC^2=AB\cdot BC\)
b) Tia BD cắt (A) tại P; một đường thẳng qua D cắt (A) tại M, cắt (O) tại N. C/M tg DPM đồng dạng tg DBN
Theo dõi (0) 1 Trả lời -


tìm độ dài cạnh tam giác ABC đều nội tiếp đường tròn(O;R)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có BC = a, CA = b, AB = c. Gọi S là diện tích của tam giác. CMR nếu (a+b+c)(b+c-a) = 4S thì tam giác ABC vuông tại A.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có ba góc nhọn, nội tiếp đường trong tâm O và AB < AC. Vẽ đường kính AD của đường tròn (O). Kẻ BE và CF vuông góc với AD ( E, F thuộc AD). Kẻ AH vuông góc với BC ( H thuộc BC)
a) chứng minh bốn điểm A, B, H, E cùng nằm trên một đường tròn
b) chứng minh HE song song với CD
c) gọi M la trung điểm của BC. Chứng minh ME = MF
Theo dõi (0) 1 Trả lời -


Chứng minh BC là tiếp tuyến của đường tròn (I,IA)
bởi Lan Ha
 16/01/2019
16/01/2019
Cho hình thang vuông ABCD có góc A=góc D=90 độ.Tia phân giác góc C đi qua trung điểm I của AD.
a.Chứng minh BC là tiếp tuyến của đường tròn (I,IA).
b.Cho AD=4cm.Tính AB.CD.
c.Gọi H là tiếp điểm của BC với đường tròn (I),K là giao điểm của AC và BD.Chứng minh KH//DC.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC vuông
bởi Sasu ka
 16/01/2019
16/01/2019
1: Cho (O;R)đường kính AB. Gọi C là điểm thuộc đường tròn (Ô) sao cho AC<BC.
a,Chứng minh tam giác ABC vuông
b, Tiếp tuyến tại A và C của (O) cắt nhau tại D. Chứng minh: OD vuông góc AC
c, Gọi H là giao điểm của OD và AC . Chứng minh 4.HO.HD=ACmũ2
d, Qua O vẽ đường thẳng vuông góc với BC tại K cắt tia AC tại M. Chứng minh: MB là tiếp tuyến của đường tròn (O)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 44 trang 107 SBT Toán 9 Tập 2
Bài tập 45 trang 107 SBT Toán 9 Tập 2
Bài tập 47 trang 108 SBT Toán 9 Tập 2
Bài tập 48 trang 108 SBT Toán 9 Tập 2
Bài tập 49 trang 108 SBT Toán 9 Tập 2
Bài tập 50 trang 108 SBT Toán 9 Tập 2
Bài tập 51 trang 108 SBT Toán 9 Tập 2






